|
|||||||||||||||||||||||||||||||||||||||||
PN:
Pannumériques
![]()
|
NOMBRE 123 456 789 Le pannumérique: nombre formé de tous les chiffres dans l'ordre. Le
pannumérique (direct)
123456789 Le
pannumérique retourné 987654321 Un
pannumérique sans 0 321456987 Un
pannumérique avec 0 3214569870 Tous les
nombres formés par permutations de ces neuf chiffres sont divisibles par 9. Toutes les
additions, soustractions et multiplications comportant tous ces chiffres
une fois ou k fois chacun donnent un résultat en multiple de 9. |
Retour au DicoNombre
123456789 / Voir Partitions pannumériques

Voir Pannumérique et son
retourné / Divisions des pannumériques et des
retournés
|
|
||||||||||||||||||||||
|
Voir |
|||||||||||||||||||||
Voir Carré de 123456789
|
Preuve par neuf
En effet: 1 + 2 + 3 + 4 + 5 +
6 + 7 + 8 + 9 = 45
Multiple de ce nombre 123 456 789 x 1 = 123 456 789 2 =
246 913 578 3 =
370 370 367 4 =
493 827 156 5 =
617 283 945 6 =
740 740 734 7 =
864 197 523 8 =
987 654 312 9 = 1 111 111 101 10 = 1 234 56 7 890 11 = 1 358 024 679 12 = 1 481 481 468 13 = 1 604 938 257 14 = 1 728 395 046 15 = 1 851 851 835 16 = 1 975 308 624 17 = 2 098 765 413 18 = 2 222 222 202 19 = 2 345 678 991 20 = 2 469 135 780
|
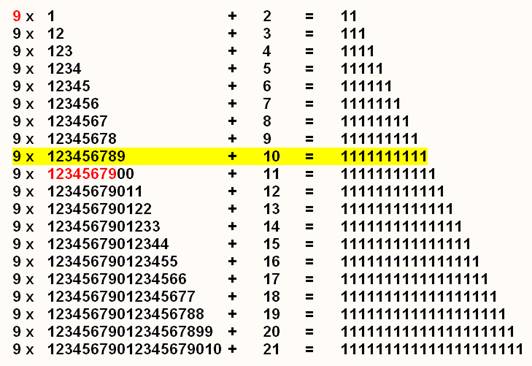
|
1 111 111 101 = 9 x 123 456 789 111 111 102 = 9 x 123 456 78 11 111 103 = 9 x 123 456 7 1 111 104 = 9 x 123 456 111 105 = 9 x 123 45 11 106 = 9 x 123 4 1 107 = 9 x 123 108 = 9 x 12 |
La somme des chiffres de ces produits est égale à 9
comme pour toutes les multiplications par 9 d'un nombre croissant. >>> |
|
987 654 321×09 = 08 888
888 889 987 654 321×18 = 17 777
777 778 987 654 321×27 = 26 666
666 667 987 654 321×36 = 35 555
555 556 987 654 321×45 = 44 444
444 445 987 654 321×54 = 53 333
333 334 987 654 321×63 = 62 222
222 223 987 654 321×72 = 71 111
111 112 987 654 321×81 = 80 000
000 001 |
Produit avec les multiples de 9. |
|
et son retourné 987654321 |
|
|
Relation (9 x 123 456 789) – 123 456 789 = 987 654 321 – 9 8 x 123 456
789 = 987
654 321 – 9 Huit fois le nombre
pannumérique est égal à son retourné moins neuf. Objet
d'un motif amusant
|
|
|
Autre
relation 9 x 123 456 789 = 1 111 111 101 9 x 123 456 789 = 1 111 111 111 –1 – 9
Neuf fois le nombre
pannumérique plus neuf égal un repunit Objet
d'un motif amusant
|
Voir Multiplications
avec pannumériques
|
|
|
|
ADDITIONS
& SOUSTRACTIONS Tous les chiffres en
trois opérations arithmétiques 7
+ 1 = 8; 9 - 6 = 3; 4 x 5 = 20 La plus petite somme
de nombres premiers 47
+ 61 + 89 + 2 + 3 + 5 = 207 Sommes en tiers 192 219 273 327 +384 +438 +546 +654 576 657 819 981 Ex: 384 = 2 x 192; 576 = 3 x 192 =
192 + 384 Sommes en
progression arithmétique de raison 9 243 341 154 317 216 215 318 235 675 586 782 628 738 748 654 746 918 927 936 945 954 963 972 981 Progression arithmétique: 918 + 9 = 927; + 9 = 963; etc. Soustractions, avec et sans le zéro 9 876 543 210 987 654 321 – 0
123 456 789 – 123 456
789 9 753 086 421 864 197 532 |
|
|
Pairs et impairs -
Égalité
Multiples (x1, x2,
x3) 192 219 273 327 384 438 546 654 576 657 819 981 Multiples (x1, x2) [6729, 13458], [6792, 13584], [6927,
13854], [7269, 14538], [7293, 14586], [7329, 14658], [7692, 15384], [7923,
15846], [7932, 15864], [9267, 18534], [9273, 18546], [9327, 18654] Multiplications
pannumériques
927 402 715 297 x 63 x 39 x 46 x 54 58 401 15 678 32 890 16
038 Fractions avec tous
les chiffres 2/4 = 3/6 = 79/158 3/6 = 7/14 = 28/58 3/6 = 9:18 = 27/54 2/6 = 3/9 = 58/174 .2/1=.6/3 = 97/485 Notation anglaise Multiplication par 6 6
x 32 547 891 = 195 287 346 6
x 94 857 312 = 569 143 872 Produit par 12 123 456 789 x 12 = 148 148 1468 123 456 78 x 12 = 148 148 136 123 456 7 x 12 = 148 148 04 Le nombre et son
retourné 123 456 789 x 989 010 989 = 122 100 120 987
654 321 |
|
Carrés avec tous les
chiffres, avec et sans le zéro
9
814 072 356 = 99 066² le plus grand 139
854 276 = 11 826² le plus petit 923
187 456 = 30 384² le plus grand Voir
son calcul Table des nombres pannumériques carrés dont 30
sans zéro et 83 avec
En admettant les
doublons de chiffres, on a, par exemple: 34273² = 1174638529 (le plus petit à
dix chiffres, ou le plus grand à dix chiffres: 98921² = 9785364241. Ils sont une
infinité. Tous les chiffres
dans le nombre et son carré 321
489 = 567² 729
316 = 854² Différence de carrés
(chiffres jusqu'à 7) 617
284² - 617 283² = 1 234 567 Différence de cubes
(chiffres jusqu'à 7) 6423
– 6413 = 1 234 567 (264
609 288 – 263 374 721) RACINES 12345678987654321
= 111111111² >>> 123456789
= 11111,111060555555440… |
Voir Nombres
pannumériques puissants / Autres Amusements
pannumériques
|
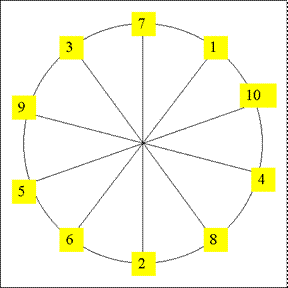
GÉOMÉTRIE
Voir autres formes
en 192 |
|
Palindromes pannumériques |
|
|||||||||||||||||||||
|
Le nombre 102345698 7 896543201 est: Nombres palindromes voisins
Remarque
Amusement 987
789 / 111 = 88 99 987654
456789 / 111 = 889 77 87 899 987654321
123456789 / 111 = 889 778 66 76 787 899 987654321012
210123456789 / 111 = 889 778 667 5785 676 787
899 987654321012345
543210123456789 / 111 = 889 778 667 578 68 96
785 676 787 899 987654321012345678
876543210123456789 / 111 = 889 778 667 578 689
80 07 896 785 676 787 899 Résultats
avec des nombres au-dessus ou égaux à 5, et qui se répètent en rythme
pseudo-palindromique. |
||||||||||||||||||||||
![]()
|
Suite |
|
|
Voir |
|
|
Aussi |
|
|
DicoNombre |
|
|
Site |
Voir le site
complet sur ce sujet de Patrick De
Geest
|
|
Cette page |
![]()