|
|||||||||||||||||||||||||||||
![]()
|
NOMBRES avec des 1 uniquement Complexité des nombres Comment
écrire tous les nombres
avec un minimum de nombres "1" et avec des opérations ne comportant
que des additions et des multiplications. Les
parenthèses sont autorisées. La concaténation (repunit)
est exclue. La quantité minimale de uns est appelée complexité du nombre. Exemple
|
Il existe
d'autres définitions de la complexité
et notamment celle des nombres
|
|
||
|
Ce type
de problème a été posé sous le titre les UNS de Germain au championnat des
jeux mathématiques et logiques et il a été publié dans 7x7 énigmes
mathématiques pour tous, Éditions POLE – 2001 . Le défi
était: écrire 99 avec le minimum de uns et les symboles d'addition et de
multiplication et les parenthèses.
|
On
retrouve le problème général dans les articles anglo-saxons sous cette forme: La complexité
d'un nombre n est la quantité minimale de uns nécessaire pour le représenter
en utilisant les additions, les multiplications et les parenthèses. The complexity of an integer n is the least number
of 1's needed to represent it using only additions, multiplications and
parentheses. Cette
notion a été introduite en 1953 par Kurt Mahler et Jan Popken,
étudiée par John Selfridge, puis popularisée par
Guy. |
|
|
|
|
|
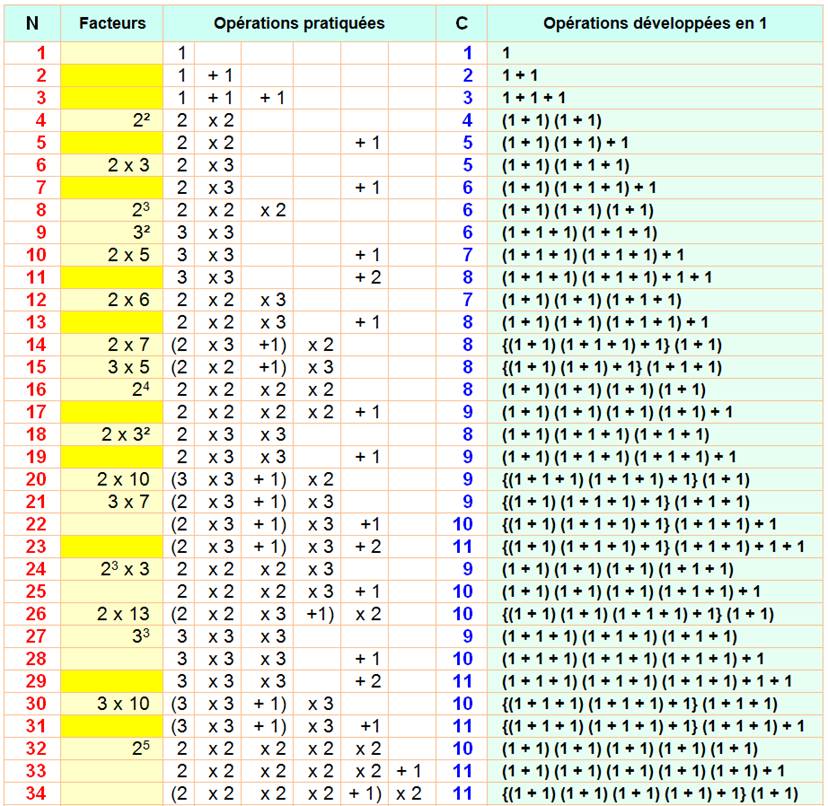
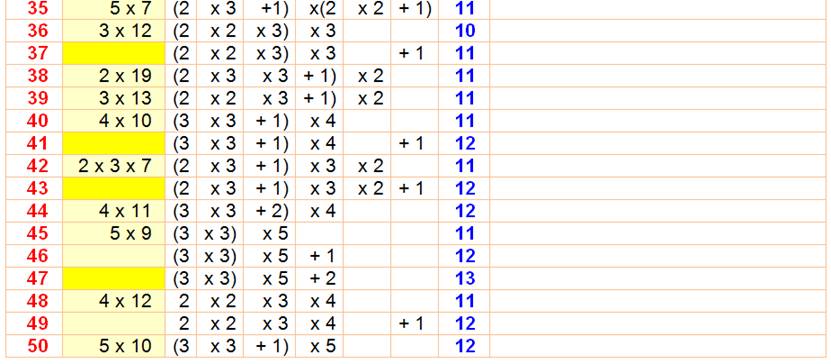
Exemple
de lecture: 7
est un nombre premier (jaune) qui peut se calculer avec l'opération 2 x 3 +
1, qui, traduite avec des uns, donne (1 + 1 ) ( 1 +
1 + 1) + 1, soit six fois le nombre 1; la complexité (C) est égale à 6.
|
|
|
Présentation
avec calcul direct de la complexité Exemple
de lecture: 50
est égal à 5 x 10. Le calcul de la complexité se fait en ajoutant les
complexités des facteurs: C(5) = 5 et C(10) = 7, soit C(50) = 5 + 7 = 12. Prenons
54 = 2 x 33 qui conduit à 2 + 3 x 3
= 11. |
Voir Tables – Index
Allure du graphe
complexité (C(n) en fonction des nombres n

|
|
||
|
Valeur de
n pour laquelle la complexité est maximale. Pour tous
les nombres jusqu'à 10 000, la complexité ne dépasse pas 30 et cette valeur
est atteinte dès n = 6 299. |
|
|
|
|
||
|
La
complexité est bornée par:
Lecture du tableau n = 10 000 C(10 000) = 28, mais avant, la complexité est
montée jusqu'à 30. Le calcul
des bornes donne: min =
25,14 arrondi au plancher 25. max =
39,88 arrondi au plafond 40. |
Si le
nombre comporte k zéros, la borne supérieure est égale à 10k. |
|
|
|
||
|
Si n = a
+ b ou a.b, alors C(n) =
min { C(a} + C(b) } |
C(n +
m) C(n .
m) |
|
La suite dépasse le cadre de ce site
et peut être lue sur les pdf indiqués en référence
![]()
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
|
|
|
Sites |
|
|
Cette page |
![]()