|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Les quatre opérations – Débutant
Multiplications et divisions
par 10, 100 …
/ Évaluation de CM1 / Brève 69
– Multiplication
Notations de la
multiplication
![]()
|
Quel âge avez-vous,
madame? – Eh bien, je compte: je me suis marié à 20
ans, mon mari en avait 30. Il en a
maintenant le double, j'ai donc 40 ans. |
Voir Pensées
& humour
|
MULTIPLICATION Comment aborder les multiplications en aiguisant son
esprit ? La multiplication -
La multiplication =
addition répétitive 10
x 3 = 3 + 3 + 3 + 3 +
3 + 3 + 3 + 3 + 3 + 3 (10 fois) -
Une histoire de paquets:
-
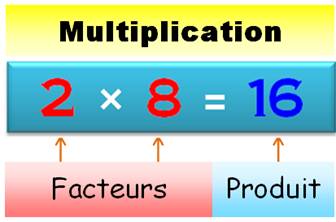
Le résultat P est
nommé le PRODUIT.
Comme il est possible de multiplier dans un sens comme
dans l'autre (2 x 8 = 8 x 2), inutile de s'embarrasser avec les mots multiplicande
et multiplicateur,
utilisez le mot facteur. Voir Puristes |
Voir
Les quatre opérations – Junior
|
Sauriez-vous
faire cette opération? Multipliez tous les chiffres du clavier de votre
téléphone. Quel est le résultat? |
|
Un
nombre appelé N, car encore inconnu. Multiplié par 2, c'est un nombre à deux
chiffres; multiplié par 3 c'est un nombre à trois chiffres. Qui est N ?
Sont-ils plusieurs à partager cette propriété?
|
Le saviez-vous?
|
Vous
savez multiplier par 2, alors vous savez faire toutes les multiplications,
même les plus compliquées; pas besoin de table! >>> |
![]()
|
|
|
|
On peut dire aussi:
ou aussi:
|
|
|
|
|
|
Initiation
aux multiplications via les diviseurs
d'un nombre
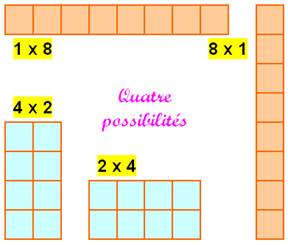
8/1 = 8 8/2 = 4 8/4 = 1 8/1 = 8 soit 4
rectangles. Nous avons créé quatre multiplications qui donnent le même
résultat.
12/1 = 12 12/2 =
6 12/3 =
4 12/4 =
3 12/6 =
2 12/1 = 12 soit 6
rectangles. Nous avons créé six
multiplications qui donnent le même résultat. |
|
|
plusieurs
multiplications peuvent donner le même résultat 2 x 6
= 3 x 4 = 12 l'ordre
des termes de la multiplication est sans importance 3 x 4
= 4 x 3
multiplication
et division sont les deux faces de la même opération 3 x 4
= 12 et 12 / 4 = 3 |
Voir Les quatre manières de symboliser une
multiplication (2x3 = 2*3 = 2![]() 3;
ab)
3;
ab)
|
Ma
petite-fille (10 ans) me pose une colle: Papy si je te dis 210, est-ce que tu
sais faire l'opération Pénélope. Je donne ma langue au chat! Facile, regarde: 210 21 x 10 21 x
5 x 2 7
x 3 x
5 x 2 14 x
3 x 5 14 x 15 210 Son
professeur des écoles a tout simplement baptisé comme cela cet exercice de
factorisation propice à s'entraîner à la table de
multiplication. Au centre, on trouve la factorisation première du nombre;
impossible de décomposer plus finement. Ces quatre nombres (2, 3, 5, 7) sont
dits: nombres premiers. Pénélope attend
longuement le retour d'Ulysse.
Les prétendants sont nombreux tant elle est belle. Elle prétend ne pas
pouvoir donner suite tant que le voile qu'elle tisse ne sera pas terminé. Or,
elle défait la nuit ce qu'elle a tissé le jour. La toile de Pénélope est
ainsi devenue une expression pour signifier un travail laborieux mais sans
fin. |
Voir Pages découvertes juniors
Multiplication des chiffres sans retenue

Voir Nombres
fluets
|
|
|
|
Le
même jeu, mais avec la liberté de superposer les carrés
On
peut former 4 rectangles en plus des 2 carrés.
Avec
les 3 grands carrés du départ, je forme 4 petits
carrés. |
|
|
Deux
nombres dont la somme est constante: A + B = K. La
valeur maximale du produit P est atteinte lorsque A = B. Exemple
Lorsque
deux champs, un carré et l'autre rectangulaire, ont le même périmètre, celui qui
couvre la plus grande surface est le champ carré. Exemple ("l" est la largueur
inconnue du rectangle)
|
Voir Carré et rectangle / Équation avec somme et produit
Le saviez-vous ?
|
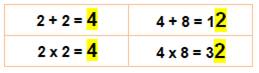
Deux
seuls cas (en jaune) où les unités de la somme et celles du produit sont
identiques:
|
Voir Addition
et multiplication
|
|
|
|
Soit
la table de multiplications des nombres de 1 à 9. Sur
chaque ligne, prenez un nombre dans une colonne différente. Le
produit de ces neufs nombres est toujours le même.
À
droite, on montre quatre exemples:
Explication Aucun
mystère ! Chaque
nombre du tableau est la multiplication de deux nombres:
Le
produit qui en résulte est constitué de tous ces nombres, et cela dans une
permutation ou une autre. Produit magique Il
vaut: (1 × 2 × … × n)² = n!² Liste:
1, 4, 36, 576, 14400, 518400, 25401600, 1625702400, 131681894400, 13168189440000,
1593350922240000, 229442532802560000, 38775788043632640000,
7600054456551997440000, 1710012252724199424000000, … Ce
sont les quantités de permutations
telles que qu'un nombre pair est suivi d'un
nombre plus grand; ou par un nombre plus petit; même chose pour les
impairs. Généralisation Cette
propriété est valable pour toute sous-grille carrée extraire de la table de
multiplication et cela dans n'importe
ordre et même avec des nombres
différents en ligne et colonne.
|
|
Voir Brève
48-940 / Addition dans la table d'additions
|
|
|||
|
|
(2 x
3) + 2 2 x
(3 + 2) |
=
(6) + 2 = 8 = 2 x
(5) = 10 |
|
|
Notez
que
le signe " x" est omis devant une parenthèse |
2 x (3 + 2) |
= 2 (3 + 2) |
|
|
|
(1 + 2) (3 + 4) (5 + 6) = 3 x 7
x 11 = 231 1 + (2 x 3)
+ (4 x 5) + 6 = 1 + 6 + 20 + 6 = 33 |
|
Notez que le produit est prioritaire sur l'addition
(c'est la multiplication qui est la plus forte et qui l'emporte) Il
est inutile de placer des parenthèses pour isoler un produit |
1 + (2 x 3) + (4 x
5) + 6 = 1 + 2 x 3 +
4 x
5 + 6 = 1 + 6 + 20 + 6 = 33 |
|
Rappel: le produit est le résultat de la multiplication. Comme la somme est le résultat de l'addition. |
|
|
{(1 + (8-3))
(3 + 4) + 2 x
3} (5 + 6) = {(1 + 5)
(7) + 2 x
3} (11) = {(6) (7)
+ 6} (11) = {42 + 6} (11) = {48} (11) = 528 |
|
(+) (+) = (+) (+) (-) = (-) (-) (+) = (-) (-) (-) = (+) |
{2 x (-4)} { 10
- 2 + 3 x 4} {(-4)(-2) – 3} = (-8) { 8 + 12} {8 – 3} = (-8) { 20} {5} = - 800 |
|
|
|
|
EXEMPLE
TRÈS SIMPLE pour commencer
Résultat 4
x 12 = 48 EXEMPLE
SIMPLE avec deux chiffres
Notez bien que le 24 = 20 + 4; Résultat 24
x 12 = 288 EXEMPLE
SIMPLE avec trois chiffres
Résultat 124
x 222 = 27 528 EXEMPLE avec le calcul d'un carré bestial En jaune clair, on donne le résultat
brut de l'addition, puis en jaune foncé, la somme avec les retenues.
Notez le résultat que rien dans l'opération posée
ne laissait soupçonner. Voir
Nombre
81 619 / Nombre 666 (de la
bête) / Carrés à
chiffres répétés EXEMPLE avec le
calcul d'un cube qui aime les 9
|
|
Voir Autres
exemples / Nombre
199 et Nombre
99 (motifs itératifs)
Multiplication avec la trigonométrie
/ Multiplication de itérative
Anglais pour multiplication
posée: long multiplication
|
La configuration en croix et la configuration en F sont
uniques et, curieusement, avec le chiffre 5 pour les deux. |
|
Voir Cryptarithmes à
multiplications
|
|
|
|
Quels sont les multiplications qui donnent un produit
terminé par un 0, un 1 … Les chiffres des unités sont très inégaux. Le 3 et
le 7 ne sont produits qu'une seule fois (hors la multiplication par l'unité).
Pour le 1 et le 9, ce n'est guère mieux. Ce sont les 4 et 6 qui détiennent le
record.
On note (ou on se souvient) que seul le produit de deux
nombres impairs
est impair, d'où leur rareté: 15 impairs (en jaune) contre 30 pairs. |
|
Voir Chiffres / Unités des puissances / Persistance multiplicative
|
|
||
|
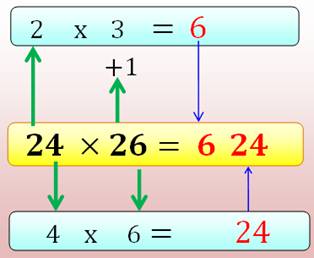
Un exemple Voyez cette multiplication: 24 x 26 = 624. Elle marche à tout coup lorsque:
Note: si le produit des unités ne dépasse pas 10,
placer un 0 intercalaire. |
26 x 24 = 624
Autres exemples 82 x 88 = 8 x (8+1) / 2 x 8
= 72 16 11 x 19 = 1 x 2 / 1 x 9
= 2 09 |
|
|
Explications Un nombre
à deux chiffres peut s'écrire A = 10 d + u (10 fois le chiffre des dizaines plus le chiffre des unités) Le second
s'écrit avec le même chiffre des dizaines et son chiffre des unités est égal
à 10 – u. Le produit
est développé puis factorisé. Le produit
d(d+1), multiplié par 100, prend place comme nombre de centaines; le produit
u(10-u) est bien le produit des deux chiffres unités. |
A = 10d + u et B = 10d + (10 –
u) A.B = 100d² +
10du + 10(10–u) + u(10–u) = 100d² + 100d + 10u – u² = 100 d(d+1) + u(10-u) |
|
|
Cas des carrés des nombres terminés par 5
Le calcul mental des carrés en …5 est très simple. Il peut être étendu à plus de deux
chiffres. Le calcul mental devient plus difficile, sauf pour les cas connus
comme la multiplication mentale
par 11. Même chose pour les unités
complémentés à 10. |
25 x 25 = 2 x 3 / 5 x5
= 6 25 65 x 65 = 6 x 7 / 5 x5 =
42 25 115 x 115 = 11 x 12 / 5 x 5
= 132 25 112 x 118 = 11 x 12 / 2 x 8
= 132 16 |
|
|
Quelques multiplications magiques Notez que: 14 x 16 = 224 = 16 x 14. |
|
|
Voir Autres multiplications
magiques
|
|
||
|
La commutativité en question … |
Certains voudraient introduire une différence entre les deux manières
de transformer une multiplication en additions. 3 x 5 = 5 x 3 = 15 Il y a égalité, mais y-a-t-il équivalence ? >>> |
|
|
Multiplication des chiffres du clavier Bravo!
Vous n'avez pas oublié le 0, et le produit complet est donc nul. Sans
le 0, nous aurions eu ce qui s'appelle une factorielle:
1 x 2 x 3 x 4 x 5 x 6 x 7 x 8 x 9 = 9!
= 362 880. |
|
Le nombre N inconnu Problème Un
nombre appelé N, car encore inconnu. Multiplié par 2, c'est un nombre à deux
chiffres; multiplié par 3 c'est un nombre à trois chiffres. Qui est N?
Sont-ils plusieurs à partager cette propriété? Exploration Je
choisis N = 40, par exemple. Alors
2 x 40 = 80 (2 chiffres) et 3 x 40 = 120 (3 chiffres). Le
nombre 40 répond à la question. Solution Les
nombres à deux chiffres commencent à 10 et finissent à 99. Divisé
par 2, nous avons les limites de N: entre 5 et 49. Les
nombres à trois chiffres commencent à 100 et finissent à 999. Divisé
par 3, nous avons les limites de N: entre 34
et 333. Pour
obtenir les deux conditions ensemble, il faut que N appartienne à la fois aux
deux plages. N doit commencer à 34 et finir à 49. De
N = 34 à N = 49, il y a 16
possibilités. (Attention: 49 – 34 = 15
qui donne le nombre d'intervalles entre 49 et 34; il faut ajouter 1 pour
avoir la quantité de nombres) En savoir plus N
multiplié par 3 donne un nombre à trois chiffres. N
multiplié par 4 donne un nombre à quatre chiffres. Combien
de nombres N? Les
limites de la plage possible sont Pour
3: 34 à 333 et pour 4: 250 à 2498 Plage
commune: de 250 à 333, soit 333 – 250 + 1 = 84 possibilités. Table des possibilités selon la quantité
de chiffres
|
![]()