Nombres Imaginaires, introduction

NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 08/12/2022 Orientation générale DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Nombres complexes
Débutants Complexes	Général				Glossaire Complexes
INDEX COMPLEXES	Introduction	Complexes		Quaternions	Octavions
	Historique	Factorisation		Trois Algèbres	Cyclotomique
	Cours de terminale		Exercice bac 2018		RADICAL
		Sommaire de cette page >>> Approche >>> Familles des nombres complexes >>> Algèbre, géométrie & topologie >>> Anglais

Voir Nombres carrés / Constante Pi / Nombre 4

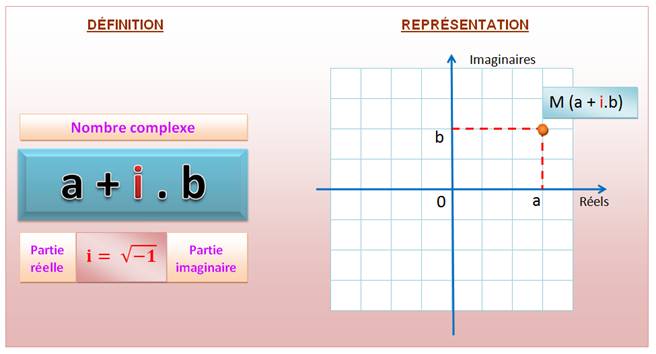
NOMBRES COMPLEXES

Les tentatives pour résoudre les équations du troisième degré, faisant appel aux racines carrées de nombres négatifs, ont conduit à l'invention des nombres complexes.

Cette invention, sous ses multiples formes, se révélera très utile pour exécuter des calculs dans de nombreux domaines scientifiques, notamment l'électronique. En fait, le nombre complexe est roi dans tous les domaines où ça tourne ou ça alterne. Le complexe s'est également révélé fécond dans le monde des fractales

Sur cette illustration, le point M a pour coordonnées x = 3 et y = 2. Il représente le nombre complexe 3 + 2i

Nombres pas si complexes! Du moins au début …

La dénomination "nombre complexe" n'est pas très heureuse, car un débutant peut en éprouver un sentiment de blocage. Or, il s'agit tout simplement d'un couple de nombres classiques liés par un symbole qui indique qu'un des nombres matérialise une direction, alors que l'autre matérialise une direction perpendiculaire.

Les nombres classiques sont des nombres-ligne;

Les nombres complexes sont des nombres-plan.

Il est vrai que l'utilisation avancée des nombres complexes fait appel à la trigonométrie et aux exponentielles et devient vite une affaire de connaisseurs.

Approche

Un imaginaire bien utile

La lettre "i "est l’initiale du mot imaginaire.

Elle est utilisée pour caractériser un nombre singulier, bien utile, mais sans existence réelle.

Par définition:

ou autrement dit i est (symboliquement) la racine carrée de –1:

Quel est le nombre le plus moche? −1 car il est hideux.

Avec ce simple nouveau nombre, il s’agit là, bel et bien, de la construction d’un nouveau monde de nombres aux vertus extraordinaires:

Le monde des nombres imaginaires (purs) lorsqu'ils sont seuls (5i)

Le monde des nombres complexes, lorsqu'ils sont deux (4 + 5i). Le nombre 4 est la partie réelle et le nombre 5 est la partie imaginaire du nombre complexe.

Note: pour ne pas confondre i intensité et i la racine de – 1, les électroniciens utilisent j pour symbole de racine de – 1. Par contre, en maths, j est l'une des racines cubiques de 1. Les logiciels de calcul utilisent le i majuscule.

Voir Notations

De façon imagée

Les nombres classique (1,2, 3, …5, 666… Pi …) se visualisent facilement en ligne, en les reportant sur une règle graduée.

Avec les nombres complexes, on étend le territoire de la ligne à la surface.

Ces nombres constituent un outil pratique pour résoudre des problèmes en électricité, en fait, partout où il y a du mouvement, des ondes.

Amusement

Voir Identité remarquable / Racine de 2 / Est-ce que i est irrationnel ?

Familles des nombres complexes
Entiers	Les nombres entiers sont les nombres usuels, utilisés pour compter la quantité de bêtes dans le troupeau ou toute autre chose.
Fractions	Les Grecs pensaient que toute mesure pouvait se faire avec des fractions: les nombres rationnels.
Irrationnels	L'école de Pythagore découvre que la racine de 2 ne peut être une fraction! C'est une valeur incommensurable, un nombre irrationnel.
Réels	Les nombres réels sont tous les nombres possibles: ceux vus ci-dessus, en y ajoutant d'étranges nombres dits transcendants.
Complexes	Comment résoudre le cas des racines des entiers négatifs? On a trouvé pratique de poser: . Les nombres complexes sont formés de deux nombres réels ajoutés dont l'un est multiplié par i. Ils sont représentés par un point sur le plan. Ces nouveaux nombres se sont avéré solution pratique de nombreux problèmes.
Quaternions	Pourquoi ne pas passer du plan au volume, de la dimension 2 à 3? C'est l'invention des quaternions, formés de quatre nombres ajoutés, et de son algèbre particulière.
Autres Algèbres	Peut-on généraliser et trouver d'autres types de nombres, d'autres types d'algèbres? Non, répond Frobenius: il n'y a que les réels, les complexes et les quaternions si on veut conserver certaines propriétés de ces nombres (multiplication, en particulier).
Octavions	On peut, néanmoins, former d'autres nombres, mais en laissant tomber certaines propriétés. Les octavions sont formés avec huit nombres ajoutés.
Sédénions	Après les nombres complexes (algèbre à 2 dimensions), les quaternions (4), les octavions (8), voici les sédénions (16).
Cyclotomiques	On a été amené à considérer la racine carrée de – 1. Et pourquoi pas la racine nième de – 1. C'est le monde des nombres cyclotomiques.

Voir Développements sur les types de nombres

ALGÈBRE, GÉOMÉTRIE & TOPOLOGIE

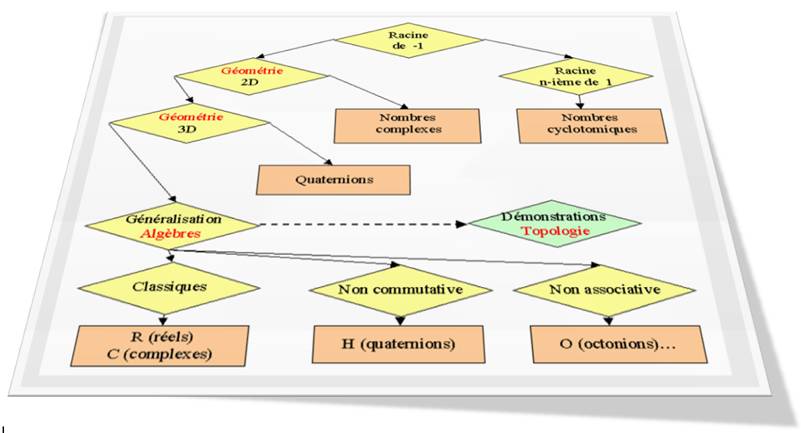
Tout est parti de la racine carrée de – 1
pour arriver à des représentations géométriques,

puis à des tentatives de généralisations des algèbres.

Pour culminer, au XX^e siècle, à la recherche de démonstrations sur l'existence et la quantité possibles d'algèbres. Ces démonstrations faisant une incursion profonde dans un nouveau domaine ardu, la topologie.