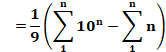|
Édition du: 17/06/2023 |
|
INDEX |
REPDIGITS |
|||
![]()
|
SOMMES de REPDIGITS La somme des
repdigits successifs offre de singuliers motifs. Occasion de s'exercer à
calculer la somme et établir une formule. |
||
|
|
Sommaire de cette page >>> Cas des repunits – Valeurs des sommes >>> Cas des repdigits – Valeurs des sommes >>> Calcul de la somme des repunits >>> Calcul de la somme des repdigits en 6 >>> Calcul de la somme des repdigits en k >>> Somme des inverses |
Débutants Glossaire |
|
Observation La somme des
repunits successifs (un chiffre, deux chiffres, …) produit un motif répétitif
formé principalement de la succession des chiffres. |
|
|
Voir Brève
764
Somme des
repdigits successifs en 2 à 9

Accès
à ces nombre: DicoNombre
|
Problème Calculer la somme de ces nombres en
1. L'indice n indique que le nombre est
répété n fois (n > 1). |
Somme Sn = 1 + 11 + 111 + … +
1111n
|
||
|
Mise en évidence de progressions
géométriques (PG) de raison 10. |
Sn = 1 + (1+10) + (1+10+100) + … + (1+10+100+…+10n-1) Le
dernier terme est une somme de n termes |
||
|
Chaque terme est calculé par la
formule des PG |
|
||
|
La somme de ces termes |
|
||
|
Exemple avec n = 3 : 1 + 11 + 111
= 123 |
|
||
|
Problème Calculer la somme de ces nombres en
6. L'indice n indique que le nombre est
répété n fois (n > 1). |
Somme Sn = 6 + 66 + 666 + … +
6666n |
||
|
La solution est bien entendu six fois le cas des
repunit, mais refaisons le calcul. |
Sn (6) = 6 x Sn
(1) = 6/81 (10n1 – 10 – 9n) |
||
|
Mise en évidence d'une suite
identique dans la suite. |
Sn
= (0+6) + (60+6) + (660+6) + … + (666n_10+6) Sn
= 10(6 + 66 + 666 + … + 6666n-1 ) + n x 6 Sn
= 10Sn-1 + 6n |
||
|
En remplaçant la somme précédente. |
Sn
= 10(Sn + 6666n) +
6n Sn
= 10Sn – 10 x 6666n + 6n |
||
|
Valeur de la somme. |
9Sn = 10 x 6666n
– 6n 9Sn = 6666n0 – 6n |
||
|
En cherchant à remplacer les 6 par
des 9 (9 = 2/3 de 6), puis à diviser par 9. |
9Sn
= 2/3 x (9999n0 – 9n) Sn = 2/3 x (1111n0 –
n) |
||
|
La somme des chiffres du nombre en 1
peut être calculée en remarquant que, par exemple : 1110 = 10 + 100 +
1000 |
1111n0 = 10 + 102 + 103 + ...+ 10n |
||
|
Il s'agit d'une progression
géométrique de raison 10 et de premier terme 10, pour n termes |
|
||
|
Vérification |
11110 = 10 x (10000 – 1) / 9 = 11110 |
||
|
Retour à notre somme |
|
||
|
Exemple avec n = 2 : 6 + 66 = 72 |
|
||
Voir Brève
51-1002
|
Observation Somme des repdigit en k:
|
|
|||||||||||||||||||||
|
Selon k |
|
|||||||||||||||||||||
|
Exemples |
|
|||||||||||||||||||||
|
Liste |
1,
[1, 12, 123, 1234, 12345, 123456, 1234567, 12345678, 123456789, 1234567900] 2,
[2, 24, 246, 2468, 24690, 246912, 2469134, 24691356, 246913578, 2469135800] 3,
[3, 36, 369, 3702, 37035, 370368, 3703701, 37037034, 370370367, 3703703700] 4,
[4, 48, 492, 4936, 49380, 493824, 4938268, 49382712, 493827156, 4938271600] 5,
[5, 60, 615, 6170, 61725, 617280, 6172835, 61728390, 617283945, 6172839500] 6,
[6, 72, 738, 7404, 74070, 740736, 7407402, 74074068, 740740734, 7407407400] 7,
[7, 84, 861, 8638, 86415, 864192, 8641969, 86419746, 864197523, 8641975300] 8,
[8, 96, 984, 9872, 98760, 987648, 9876536, 98765424, 987654312, 9876543200] 9,
[9, 108, 1107, 11106, 111105, 1111104, 11111103, 111111102, 1111111101,
11111111100] |
|||||||||||||||||||||
Avec
les inverses, somme infinie
|
|
Le calcul est compliqué !
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Cette page |