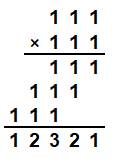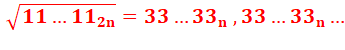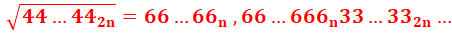|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
RACINE
CARRÉ des
nombres uniformes (repdigits) La racine carrée des nombres repdigits présente des
régularités surprenantes. Certains calculateurs prodiges, comme Gert Mittring, en font une spécialité de calcul mental. |
Angl
|
Racine des nombres palindromes
"en toit" (En référence à la symétrie par rapport au
chiffre central) Note: la racine carrée de 123456789 est
11111,111060… Amusements
sur calculette proposés par Paul
Villemin Voir Brève
de maths n° 583 / Palindromes |
n |
|
Exemple de multiplication posée
|
|
121 |
11 |
||
|
12321 |
111 |
||
|
1234321 |
1 111 |
||
|
123454321 |
11 111 |
||
|
12345654321 |
111 111 |
||
|
1234567654321 |
1 111
111 |
||
|
123456787654321 |
11 111
111 |
||
|
12345678987654321 |
111
111 111 |

Voir Brève
50-985
|
|
|
|
Le tableau est composé de neuf sous-tableaux;
chacun donne le repdigit puis sa
racine carrée avec dix chiffres signiicatifs. Exemple de lecture: racine de 111 = 10, 53565375 ….
Voir Brève
de maths 583 Observation 1 (en bleu) En distinguant, la quantité paire ou impaire de chiffres,
la racine présente des chiffres avant la virgule qui se cumulent: racine de
111 = 10,… et racine de 11111 = 105,… Même chiffres avec un 5 ajouté. Observation 2 (en rouge) Avec les chiffres qui sont des carrés (1, 4 et
9), se dessinent une particularité pour une quantité paire (2n) de chiffres:
la racine est un repdigit de n chiffres, suivi du même repdigit après la
virgule: racine de 11 = 3,3… et racine 11111 = 33,33… |
|
|
|
||
|
Repunit |
…
La racine carré d'un repdigit en 1 comportant 2n chiffres est égale à
n fois 3 virgule n fois 3. |
|
|
4–R epdigit
|
…
La racine carré d'un repdigit en 4 comportant 2n chiffres est égale à
n fois 6 virgule n fois 6, suivi de n fois 3. |
|
|
9–R epdigit
|
6 / 999,999 5 (notation pour la ligne ci-dessus) … 14 /
9999999,999999949999999999999… 16 /
99999999,999999995000000000000… … 50 / 9999999999999999999999999,99999 2n /
9n , 9n 5 La racine carré d'un repdigit en 9 comportant 2n chiffres est égale à
n fois 9 virgule n fois 9. La décimale suivante est très proche de 5. |
|
![]()
|
Suite |
|
|
Voir |
|
|
Cette page |
![]()