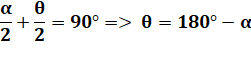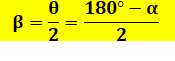NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 15/10/2023 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Maths en se divertissant
Débutants Général	BRÈVES de MATHS									Glossaire Général
INDEX Brèves Atlas des maths	Page 1	Page 10		Page 20		Page 30		Page 40			Page 50
	Page 50 (980-999)		Page 51 (1000-1019)		Page 52 (1020-1039)		Page 53 (1040-1059)		Page 54 (1060-1079)
	Page 55 (1080-1099)		Page 56 (1100-1119)		Page 57 (1120-1139)		Page 58 (1140-1159)		Page 59 (1160-1179)

Brèves et curiosités mathématiques: la millième en juin 2023

BRÈVES de MATHS – Page 51

Un millier de faits et chiffres

sur les nombres et les mathématiques

Ces pages sont dédiées à tous ceux qui veulent aborder les mathématiques en douceur et en s'amusant tout en découvrant les aspects les plus fondamentaux de cette discipline. Un parcours à picorer avec nombreux liens d'orientation vers les développements destinés à satisfaire votre curiosité.

En principe ces pages sont très abordables sans connaissances particulières de maths. Elles sont proposées dans un ordre quelconque favorisant la découverte de sujets multiples.

Anglais: Facts and figures about numbers and mathematics

1000. Nombres – Curiosités, théorie et usages
MILLE Est invariable: trois mille; mais quatre milliers. Expressions et humour Papa mille-pattes à son fils: dans la vie, ne te laisse jamais marcher sur les pieds! Jeux du quatre "4" Voir Jeu du nombre en quatre 4		Mouvements pour fêter la millième
Brèves associées	>>> Nombre 1000 – Curiosités		>>> Brèves Nombre – Index
Pour en savoir plus	>>> Nombre 1000 dans le DicoNombre		>>> Nombre 1000 et expressions

1001. Puissances pannumériques
Propriété Seuls trois nombres possèdent cette propriété: Les chiffres concaténés de deux puissances de ces nombres sont pannumériques. C'est-à-dire qu'il y a tous les chiffres de 0 à 9 et cela une seule fois. Comment calculer Cette propriété peut être détectée facilement par programmation. Il est aussi possible de la vérifier à l'aide d'un tableur. Et, cela constitue un excellent exercice à la pratique du tableur.		Avec deux puissances, tous les chiffres sont là.
Brèves associées	>>> Pannumériques et carrés		>>> Brèves Motifs – Index
Pour en savoir plus	>>> Concaténation de puissances		>>> Exercice avec le tableur

1002. Somme 1 + 11 + 111 + …

Somme en 1

1 + 11	= 12
1 + 11 + 111	= 123
1 + 11 + 111 + 1111	= 1234
1 + 11 + 111 + … + 111n
Liste de ces nombres pour n de 1 à 15	1, 12, 123, 1234, 12345, 123456, 1234567, 12345678, 123456789, 1234567900, 12345679011, 123456790122, 1234567901233, 12345679012344, 123456790123455

Somme en 6

6 + 66	= 72
6 + 66 + 666	= 738
6 + 66 + 666 + 6666	= 7404
6 + 66 + 666 + … + 666n
Liste de ces nombres pour n de 1 à 15	6, 72, 738, 7404, 74070, 740736, 7407402, 74074068, 740740734, 7407407400, 74074074066, 740740740732, 7407407407398, 74074074074064, 740740740740730

Brèves associées

>>> Somme des entiers: 1 + 2 + 3 + 4 + …

>>> Brèves Opérations – Index

Pour en savoir plus

>>> Somme de repdigits

>>> Repdigits

1003. Aire de la flèche
Description Un carré ABCD. Une flèche dont le point est le milieu du côté CD et le creux est au centre du carré. Quelle est l'aire de la flèche ? Aire de la flèche Aire du triangle AEB = ½ (12 × 12) = 72 Aire du triangle AFB = ½ (12 × 6) = 36 Aire de la flèche: 72 – 36 = 36 Autre méthode Aire de la flèche = ½ c – ¼ c = ¼ c = 144/4 = 36
Brèves associées	>>> Aire du poisson		>>> Brèves Géométrie – Index
Pour en savoir plus	>>> Aire de la flèche		>>> Aire – Index

1004. Cinq nombres à trouver

Énigme

Trouver cinq nombre entiers dont

la moyenne est 4,

la médiane est 5 et

le mode est 1.

Rappels

Moyenne: somme des valeurs divisée par la quantité.

Médiane: autant de valeurs avant et après ce nombre.

Mode: indique la valeur la plus fréquente. En cas d'égalité, il peut y avoir plusieurs modes.

Solution

Médiane 5	Nombre au centre de l'ensemble des nombres	-	-	5	-	-
Mode 1	Il y a au moins deux 1 et pas plus du fait de la présence du 5.	1	1	5
Mode unique	Les nombres 5, x et y sont uniques, croissants et distincts.	1	1	5	x	y
Moyenne 4	1 + 1 + 5 + x + y = 5x4 = 20	1	1	5	x + y = 13
	Avec x et y différents supérieurs à 5	1	1	5	6	7

Brèves associées

>>> Combinaisons de 7 parmi 15

>>> Brèves Statistiques – Index

Pour en savoir plus

>>> Vocabulaire des statistiques

>>> Statistiques débutants

1005. Nombres à chiffre dominant
Définition Les nombres à chiffre dominant sont tels que le chiffre de gauche est plus grand que tous les autres. Ex: 54321, le chiffre 5 est le plus grand de tous. Combien ? Amusant ! La quantité de ces nombres à k chiffres est égale à la somme de tous les chiffres chacun porté à la puissance k – 1. Ex: de 1000 à 9999, k = 4 et la quantité est: 1^3 + 2^3 + 3^3 + 4^3 + 5^3 + 6^3 + 7^3 + 8^3+ 9^3 = 3 035		Les 45 nombres dominants à deux chiffres 10, 20, 21, 30, 31, 32, (seuls 0, 1 et 2 sont inférieurs à 3) 40, 41, 42, 43, 50, 51, 52, 53, 54, 60, 61, 62, 63, 64, 65, 70, 71, 72, 73, 74, 75, 76, 80, 81, 82, 83, 84, 85, 86, 87, 90, 91, 92, 93, 94, 95, 96, 97, 98.
Brèves associées	>>> Nombres glissants		>>> Brèves Types de nombres – Index
Pour en savoir plus	>>> Nombres à chiffre dominant		>>> Nombres à motifs

1006. Anniversaire – Combien ?
Problème C'est un anniversaire, les copains et copines sont réunis. La moitié d'entre eux ne boit que du jus de fruit. Un tiers ne boit que du coca. Il y a 15 invités qui ne boivent ni l'un ni l'autre et personne ne boit les deux. Combien de personnes à cet anniversaire ?		Solution Personnes qui boivent du jus de fruit ou du coca: 1/2 + 1/3 = 3/6 + 2/6 = 5/6 Sachant que 15 personnes qui ne boivent rien représentent 1/6, une proportion permet de calculer la totalité des présents : T = 15 x 6 = 90.
Brèves associées	>>> Âges à deviner		>>> Brèves Énigmes – Index
Pour en savoir plus	>>> Énigmes logiques et paradoxes		>>> Anniversaires improbables ?

1007. Calculer a^5 + b^5
Problème Sachant que a + b = 1 et a² + b² = 2, calculer a^5 + b^5. D'abord, on calcule la valeur du produit ab avec (a + b)² = a² + b² + ab = 1, et on en déduit que ab = -1/2. Ensuite, les identités remarquables font l'affaire. Sauriez-vous calculer a^11 + b^11 ?		Solution
Brèves associées	>>> Comparez 99! et 50^99		>>> Brèves Opérations – Index
Pour en savoir plus	>>> Identité en somme de deux puissances		>>> Identités classiques

1008. Carré et corde du cercle
Problème Un cercle et un carré dont le côté est une corde distance d'une unité de la circonférence. Voir figure. Quelle est l'aire du carré ? Solution (figure du bas) On nomme x la longueur du côté du carré. Le diamètre du cercle vaut: x + 1. Calculs Aire du carré = 4² = 16
Brèves associées	>>> Carré et deux triangles équilatéraux		>>> Brèves Géométrie – Index
Pour en savoir plus	>>> Cordes		>>> Cercle – Index

1009. Puissances de 2 & 2^100 – 2^99 …
Somme des puissances de 2 En dernière ligne la somme (cumul) des puissances de 2. Propriété remarquable Chaque puissance de 2 est égal à la somme des puissances de 2 inférieures plus 1. Ex: 2^10 = 1 + 2^0 + 2^1 + … + 2^8 + 2^9		Calculer cette expression En rouge, mise en évidence de la propriété des puissances de 2. D'une manière générale Ex: 2^3 – 2^2 – 2^1 – 2^0 = 2^0 = 1 2^13 – 2^12 – 2^11 – 2^10 = 2^10 = 1024
Brèves associées	>>> Somme de puissances		>>> Brèves Puissances – Index
Pour en savoir plus	>>> Somme des puissances de 2		>>> Sommes

1010. Racines continues
Les racines continues sont les racines de racines d'un nombre ou d'une expression. Elles se prolongent sans fin selon un nombre répété ou un motif régulier. Dans le cas du nombre 6, le calcul est simple une fois réalisée la mise au carré de l'expression; en remarquant que la partie en rouge est égale à x. Dans le cas général avec k en racines continues, la solution de l'équation du second degré n'est un nombre entier que dans certains cas particuliers. Alors k = n(n – 1)		Racines continues de 6 Racines continues de k
Brèves associées	>>> Fraction continue à la demande		>>> Brèves Opérations – Index
Pour en savoir plus	>>> Racines continues >>> Racines continues et tous les nombres		>>> Fractions continues

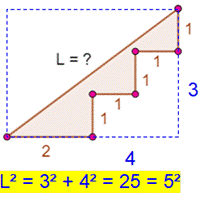
1011. Longueur de la rampe
Problème Un escalier et sa rampe. Quelle est la longueur de la rampe L ? Solution Un simple dessin donne la piste: un rectangle qui entoure l'escalier. Alors, le théorème de Pythagore entre en action. Et le calcul donne: L = √5² = 5.
Autres exemples À gauche L² = 2² + 3² = 13 L = √13 = 3,60… À droite L² = 4² + 4² = 2 × 4² L = 4√2 = 5,65 …
Brèves associées	>>> Quizz de géométrie (20 problèmes)		>>> Brèves Géométrie – Index
Pour en savoir plus	>>> Calcul de périmètres		>>> Théorème de Pythagore

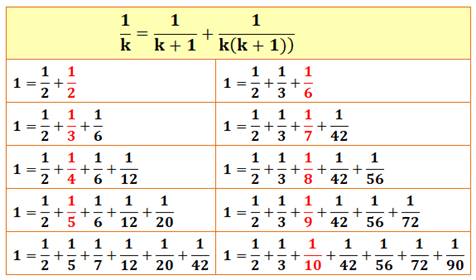
1012. Infinité de fractions égales à 1
La relation indiquée permet de transformer toute fraction en somme de deux fractions. En partant de 1 = 1/2 + 1/2 et, de proche en proche, il est possible de remplacer l'une des fractions par une somme de deux fractions. Le tableau donne des exemples. En rouge, la fraction remplacée dans la case du dessous.
Brèves associées	>>> Fraction continue à la demande		>>> Brèves Calculs – Index
Pour en savoir plus	>>> Fractions égale à 1		>>> Nombre 1 dans le DicoNombre

1013. Partage du disque
Problème Un disque. Comment obtenir N surfaces d'égales aires avec règle et compas ? Solution Partager le diamètre en N parties égales et tracer les demi-cercles comme pour cet exemple (N = 8). Justification L'aire de chaque demi-cercle est proportionnelle au carré du numéro du demi-cercle de 1 à 8. On calcule ce coefficient de proportionnalité par différence entre la partie couverte et la partie en trop.		Disque partagé en huit surfaces d'égale aire Chaque surface (sorte de S) est composée de deux demi-cercles dont on retire deux demi-cercles plus petits. L'aire de chaque surface est égale à:
Brèves associées	>>> Cercles de Ford		>>> Brèves Géométrie – Index
Pour en savoir plus	>>> Partage du cercle		>>> Constructions – Index

1014. Racines par factorisation
Méthode Comment résoudre une équation d'apparence simple ? Trouver une racine par intuition et résoudre la factorisation.		Outils Si a est une racine, alors x – a est un facteur du polynôme. L'autre facteur est un polynôme générique de degré juste inférieur dont il faudra déterminer les coefficients.
Résolution
Brèves associées	>>> Équation de l'année démystifiée		>>> Brèves Équations – Index
Pour en savoir plus	>>> Équation du deuxième degré		>>> Équations – Index

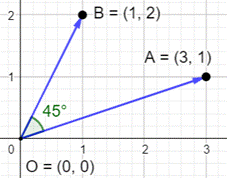
1015. Sinus et coordonnées de points
Notre problème Vous devez trouver la valeur d'un angle et vous ne connaissez que les coordonnées de points situés sur les côtés de l'angle. Comment faire ? Utiliser le produit vectoriel. Mais, quésaco ? Calcul de l'angle L'angle est connu par les segments OA et OB qui en l'occurrence sont nommés vecteurs (segments avec une flèche). Le produit vectoriel consiste en un calcul spécial avec les coordonnées des vecteurs. Il est noté: Un des ses particularités est que: sa norme divisée par le produit des normes des deux vecteurs, donne le sinus de l'angle entre les vecteurs (voir la formule). Voir le lien pour des exemples pratiques de calcul.		Sinus en fonction du produit vectoriel Calculer la valeur de l'angle AOB Connaissant les coordonnés de O, A et B, il est possible de calculer directement le sinus de l'angle avec la formule indiquée. Magique, non ?
Brèves associées	>>> Sinus et cosinus & DEMI		>>> Brèves Trigonométrie – Index
Pour en savoir plus	>>> Exemples de calcul du sinus		>>> Angles – Index

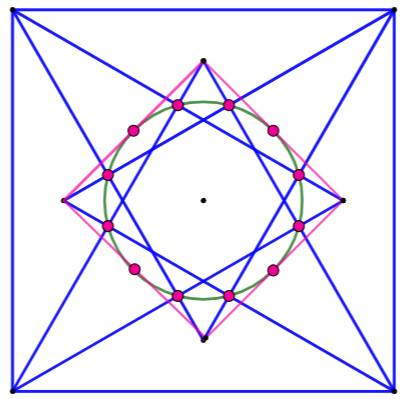
1016. Dodécagone dans le carré
Construction Un grand carré avec ses quatre triangles équilatéraux inscrits sur les côtés. Le carré rose reliant les sommets libres des triangles équilatéraux. Points rouges Ce sont les huit intersections entre triangles équilatéraux. Et, les quatre milieux des côtés du carré rose. Dodécagone Ces douze points sont cocycliques (ils sont situés sur un même cercle) et répartis régulièrement. Ce sont les sommets d'un dodécagone régulier. Démonstration Une des démonstrations utilise le calcul des angles avec le produit vectoriel tel que vu en brève précédente.
Brèves associées	>>> Dodécagone – Régions externes		>>> Brèves Géométrie – Index
Pour en savoir plus	>>> Dodécagone – Démonstration		>>> Dodécagone

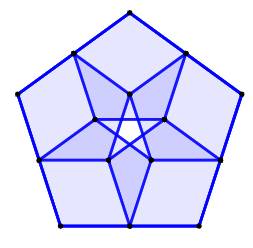
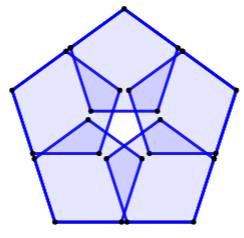
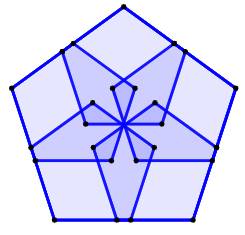
1017. Étoile dans pentagone
Construction Un pentagone. Cinq pentagones construits sur les côtés du grand. La taille des petits est ajustable.		Exemples Avec un côté égal à 0,3 fois le côté du grand, les petits pentagones sont bien espacés. Avec un côté égal à 0,5 fois le côté du grand, les petits pentagones se rejoignent et dessinent une étoile interne et une étoile médiane.
Rapport 0,3 Rapport 0,5		Rapport 0,45 Rapport 0,55
Brèves associées	>>> Pentagone – Aire avec trois triangles		>>> Brèves Géométrie – Index
Pour en savoir plus	>>> Pentagone		>>> Pentagone – Construction

1018. Angles autour du cercle
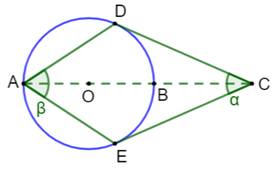
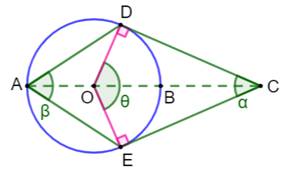
Construction Un cercle et ses deux tangentes à partir du point C. Les points D et E sont les points de tangence. Quelle est la relation ente les angles alpha et bêta ? Solution (figure du bas) Les angles en C et les angles en O sont complémentaires: Angles interceptant le même arc:
Brèves associées	>>> Angles dans trois carrés		>>> Brèves Géométrie – Index
Pour en savoir plus	>>> Angles autour du cercle – Détaillé		>>> Défis mathématiques

1019. Différences de 1 à 6
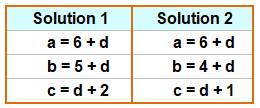
Problème Quatre nombres entiers différents: a, b, c et d. La valeur absolue de leur différence deux à deux. On obtient six nombres entiers: 1, 2, 3, 4, 5 et 6. Valeurs de a, b, c et d ? Deux solutions La plus grande différence est en haut du graphique alors que les trois plus petites sont en bas. Un petit calcul montre qu'il existe deux solutions et qu'elles sont fonctions de la valeur de d.		Relation d'ordre La flèche signifie: strictement plus grand Exemple avec d = 10
Brèves associées	>>> Divisibilité par 45 de aaaabbbb		>>> Brèves Énigmes – Index
Pour en savoir plus	>>> Différences de 1 à 6 – Explications		>>> Défis mathématiques – Index

Retour	Brèves de maths – Page 50
Suite	Brèves de maths – Page 52
Voir	Voir liens en haut de page
Cette page	http://villemin.gerard.free.fr/NombDico/aBreves/Breve51.htm