NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 23/05/2016 Orientation générale  DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique
	Forme des nombres
Débutants Nombres figurés	NOMBRES FIGURÉS			Glossaire Nombres figurés
INDEX Nombres géométriques Géométrie Nombres	Introduction	Théorie	Calcul	Tables
		TYPES un par un
		Pentagonaux	En grappe pentagonale
		Sommaire de cette page >>> Nombres heptagonaux centrés >>> Calcul de la formule – Cas de la grappe

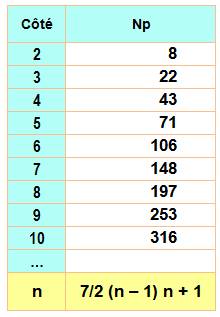
NOMBRES HEPTAGONAUX CENTRÉS

ou en GRAPPE PENTAGONALE

Nombres figurés formés sur un heptagone régulier point central.

Nombres HEPTAGONAUX CENTRÉS
Les dix premiers Ces nombres sont alternativement pairs puis impairs.		Configuration heptagonale centrée 1 8 22 Configuration en grappe pentagonale G2 = 8 G3 = 22
Formules	Sept fois le triangulaire de rang précédent plus un.
Autre formule	Exemple: N4 = 1 + 7 + 14 + 21 = 43
Propriété de convergence	La somme des rapports des nombres heptagonaux centrés avec la puissance de 2 de même rang tend vers 15
Somme des inverses

Calcul de la formule – Cas de la grappe
Trapèze du haut
Sommet	n
Base	p = n + (n – 1) = 2n – 1
Surface	p (p + 1) / 2 – (n–1) n / 2 Somme des nombres jusqu'à p, diminué de ceux au–dessus du sommet, c'est–à–dire jusqu'à n–1
Triangle du bas
Base	p – 1 Un cran en dessous de p
Surface	(p – 1) p / 2
Total des deux surfaces
NP =	p(p+1)/2 – (n–1)n/2 + (p–1)p/2
2NP =	(2n–1)(2n–1+1) – (n–1)n + (2n–1–1)(2n–1)
	4n² – 2n – n² + n + 4n² – 4n – 2n + 2
	7n² – 7n + 2
NP =	[7/2 (n–1) n ]+ 1
Autre calcul en remarquant une forme de losange tronqué
Losange :	p²
Triangle tronqué	n (n – 1) / 2
Total (Idem ci-dessus, heureusement!)	p² – n (n – 1) / 2 = (2n – 1)² – n (n – 1) / 2 = ( 7n² – 7n – 2) / 2

Retour	Nombres pentagonaux Listes des types de nombres figurés
Suite	Introduction aux nombres géométriques Théorie des nombres géométriques Pentagone et étoile à cinq branches
Voir	Calcul mental – Index Géométrie – Index Liste des noms des nombres Partition Somme des cubes des entiers TABLES de nombres Théorie des nombres
DicoNombre	Nombre 8
Sites	Voir les liens sur la page Glossaire >>> OEIS A069099 – Centered heptagonal numbers
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Geometri/HuitNbPe.htm