|
||||||||||||||||||||||||||||||||
![]()
|
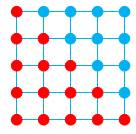
Nombres POLYGONAUX ou GÉOMÉTRIQUES ou FIGURÉS Nombres qui se prêtent à une représentation géométrique. Nom officiel; nombres figurés (figurate numbers);
on trouve aussi nombres géométriques. Les nombres polygonaux sont les nombres
dont la figure géométrique de représentation est un polygone, généralement
régulier. Les nombres polyèdraux sont représentés par des figures dans
l'espace Quantité des propriétés de ces nombres étaient
connues des Grecs et, en particulier de Pythagore. |
Voir 100 est un
phénomène géométrique / Liste
des noms des nombres figurés
Théorème des nombres polygonaux (Fermat
-1636)
|
Tout nombre entier est la somme de, au plus, k nombres k-gonal.
Dans une lettre adressée à Mersenne, Fermat
prétend disposer de la démonstration. Celle-ci n'a jamais été
retrouvée. En 1770, Lagrange prouve le cas des carrés.
En 1796, Gauss prouve le cas des triangulaires. En 1813, c'est Cauchy qui règle tous les
cas. |
Anglais: Fermat’s polygonal number theorem
Voir Brève
675
Revue de quelques propriétés typiques
|
|
||
|
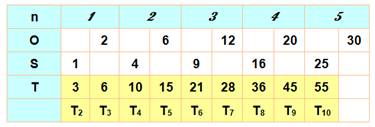
Quantité de points disposés en forme de triangle équilatéral. Tn = {1, 3, 6, 10, 15, 21 …} Un nombre triangulaire Tn
est égal à la somme des n premiers nombres. Démonstration
Voir
Démonstration
par récurrence |
Illustration
T1 =
1 T2 = 3 T3 = 6 Observez les boules ajoutées à chaque étape: T1
= 1 T2
= 1
+ 2 T3
= 1
+ 2 + 3 |
|
|
Formule en 3 T3n – 1
= 3Tn + 6 Tn – 1 Démonstration 3/2 n (n + 1) +
6/2 (n – 1) n = 1/2 (3n² + 3n
+ 6n² – 6n) = 1/2 (9n² –
3n) Or T3n-1
= 1/2 (3n – 1) (3n) |
Exemple avec n
= 5 T14 = 3 T5 + 6 T4 14x15/2 = 105 3x5x6/2 + 6x4x5/2 = 45 + 60 = 105
n = 3 => T8
= 3T3 + 6T2 |
|
|
Formule pour trois consécutifs Pour trois
triangulaires consécutifs, le central est la moyenne des deux autres à un
près. 2Tn + 1 = Tn – 1 + Tn + 1
|
Tn = {1, 3, 6, 10, 15, 21
…} 2 x 15 + 1 =
31 10 + 21 = 31
|
|
|
Passage au rang pair T2n = 3Tn + Tn
– 1 Démonstration 3 x 1/2 n (n +
1) + 1/2 n (n – 1) = 1/2 (3n² + 3n
+ n² - n) = 2n² + 2n = T2n |
n = 4 => T8
= 3T4 + T3 |
|
|
Passage au rang impair T2n+1 = 3Tn + Tn + 1 Démonstration 3 x 1/2 n (n +
1) + 1/2 (n+1) (n + 2) = 1/2 (3n² + 3n
+ n² + 3n + 2) = 1/2 (4n² + 6n + 2) Or T2n+1 = 1/2 (2n + 1) (2n + 2) = 1/2 (4n² + 6n + 2) |
n = 3 => T7
= 3T3 + T4 |
|
Voir Autres
propriétés des triangulaires / Tables de nombre triangulaires
|
|
||
|
Aussi appelé "oblongs".
Quantité de points dans un rectangle de côté n et n+1. On = {2, 6, 12, 20, 30, 42 …} Un nombre pronique On est égal à la somme
des n premiers nombres pairs. Démonstration
Autre propriété Pronique = 2 x Triangulaires On
= Tn + Tn |
Illustration
O1 =
1x2 O2 = 2x3 O3 = 3x4 Observez les boules ajoutées à chaque étape: O1
= 2 O2
= 2
+ 4 O3
= 2
+ 4 + 6 Somme de deux triangulaires
|
|
|
|
||||||||||||||||||||
|
Un nombre carré,
"square number" en anglais, est la quantité de points disposés dans
un carré (ou un losange) P4,n = Sn = {1, 4, 9,
16, 25, 36 …} Un nombre carré Sn est égal à la somme des n premiers nombres impairs. Démonstration L'illustration géométrique parle
d'elle-même: 1 + 3 + 5 +… + n = n² OK!
Mais je voudrais une démonstration |
Illustration
S1 = 1x1 S2 = 2x2 S3 = 3x3 Observez les boules ajoutées à chaque étape: S1
= 1 S2
= 1
+ 3 S3
= 1
+ 3 + 5 |
|||||||||||||||||||
|
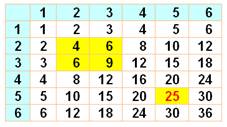
Formule de Theon de Smyrne (v70-v135) Un nombre
carré est égal à la somme de deux
triangulaires: son homologue et le précédent. Démonstration Tn + Tn – 1 = 1/2 { n(n+1) + (n–1)n } = 1/2 { n² + n + n² – n
} = n² = Sn |
Sn = Tn + Tn-1
6 + 10 =
16 = 4²
15 + 10 =
25 = 5² |
|||||||||||||||||||
|
Un nombre
carré (n²) est égal à la somme du
carré précédent (n–1)² et des deux nombres correspondants n et (n–1). Démonstration (n – 1)² + n + (n – 1) = (n² – 2n + 1) + n + (n – 1) = n²
|
Sn = Sn–1 + n + (n–1)
9 + 3 + 4 = 16 = 4² |
|||||||||||||||||||
|
Formule de Diophante et Plutarque Le carré d'un nombre
impair est égal à huit fois un triangulaire plus 1. Démonstration 8 . Tn + 1 = 8 { n(n+1) / 2 } + 1 = 4 { n² + n } + 1 = 4n² + 4n
+ 1 = (2n + 1)² = S2n+1 Voir Brève
de Math 505 |
S2n+1 = 8 . Tn
+ 1
8 x 3 + 1 = 25 |
|||||||||||||||||||
|
|
|||
|
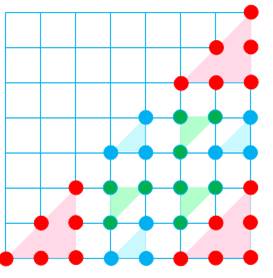
Carré (S), triangulaire (T) et pronique (O)
sont liés par les relations indiquées. Démonstration T2n = 1/2 { (2n)(2n+1) } = 2n² +
n On = n(n+1) = n² + n T2n+1 - On = n² = Sn T2n+1 = 1/2 { (2n+1)(2n+2) } =
2n² + 3n + 1 On = n(n+1) = n² + n T2n+1 - On = n² + 2n + 1 = (n+1)² = Sn+1 |
Sn
= T2n – On Sn+1 = T2n+1
– On Tableau exprimant cette relation
10 = 4 +
6 T4 = S2 + O2 15 = 9 +
6 T5 = S3 + O2 |
||
|
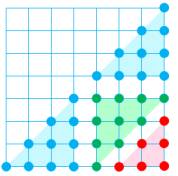
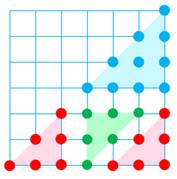
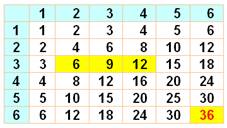
Carrés et proniques sont liés par les
relations indiquées. Illustration avec la Table de multiplication
ordinaire. La diagonale donne les carrés et, de chaque
côté, du carré les proniques. |
S2n+1 = 2
On + Sn + Sn+1 S2n = 2 Sn + On + On-1
S2x2+1 = 25 = 6 + 6 +
4 + 9 // S2x3 = 36 = 2 x 9 + 6 +
12 |
||
|
|
||
|
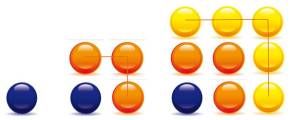
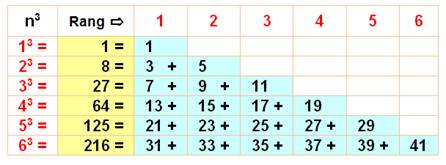
Quantité de points disposés dans un cube. 1, 8, 27, 64, 125, 216 … On peut calculer les cubes à partir
des nombres impairs. |
On écrit la suite des nombres impairs.
Chaque ligne en contient une quantité égale au nombre objet du calcul du
cube. Ainsi 33 est la somme de trois impairs.
|
|
![]()
|
|
||
|
Entier |
Somme de
3 triangulaires, de 4 carrés, de 5 pentagonaux, etc. |
|
|
Entier |
Somme de
trois palindromes (ou quatre en base2) |
|
|
Polygonaux |
Théorème
des nombres polygonaux |
|
|
Polygonaux |
En
progression arithmétique |
|
|
Polygonaux |
Produit
en croix |
|
|
Pronique |
Somme des
nombres pairs; il est pair |
|
|
Pronique |
Somme des
inverses tend vers 1 |
|
|
Triangulaire |
Somme des
entiers |
|
|
Triangulaire |
Demi-pronique |
|
|
Triangulaire |
Un sur
deux est hexagonal; ceux de rang impair |
|
|
Triangulaire
centré |
Carré |
|
|
Carré |
Somme de
deux triangulaires |
|
|
Carré |
Somme des
impairs |
|
|
Carré centré |
Quatre
fois triangulaire plus un |
|
|
Oblong |
Somme des
pairs |
|
|
|
|
|
|
Pentagonal |
Tiers de
triangulaire |
|
|
Hexagonal |
Théorème
des nombre hexagonaux: aussi triangulaires |
|
|
Hexagonal |
Somme de
triangulaires |
|
|
Heptagonal
centré |
Sept fois
triangulaire plus un |
|
![]()
|
Retour Suite |
|
|
En savoir plus |
|
|
Références |
|
|
Voir |
|
|
Cette page |
http://villemin.gerard.free.fr/Referenc/Prof/APROF/NbGeom.htm
|
![]()