NOMBRES – Curiosités, Théorie et Usages

 

Accueil                           DicoNombre            Rubriques           Nouveautés      Édition du: 13/07/2023

Orientation générale        DicoMot Math          Atlas                   Actualités                       M'écrire

Barre de recherche          DicoCulture              Index alphabétique        Références      Brèves de Maths    

         

Géométrie

 

Débutants

Général

POLY …

 

Glossaire

Général

 

 

INDEX

Géométrie

 

Polygones – Index

Polyèdres

Polytopes

Polygones – Propriétés  

Tectoèdres

 

 

Sommaire de cette page

>>> Polytopes

>>> Polytopes réguliers

>>> Autres Polytopes

 

  

 

 

 

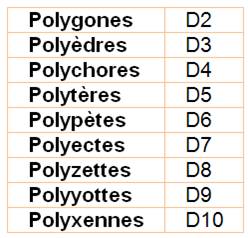
POLYTOPES

 

Polygones en dimension 2;

Polyèdres  en dimension 3;

Polytopes  en dimension 4 et plus:

     Hyper-solides en quatrième dimension, et plus…

 

Polygones et polyèdres sont aussi des polytopes de dimension 2 et 3.

 

 

Voir Nombre polytopes

 

 

POLYTOPES

 

*      Volumes en dimension 4, prolongement des polyèdres en dimension 3.

Ils ont des:

*      faces,

*      arêtes

*      sommets et, en plus,

*      des volumes en 3 dimensions appelés " cellules "

 

*      Il existe

*        6 polytopes réguliers convexes et

*      10 polytopes réguliers étoilés.

 

 

 

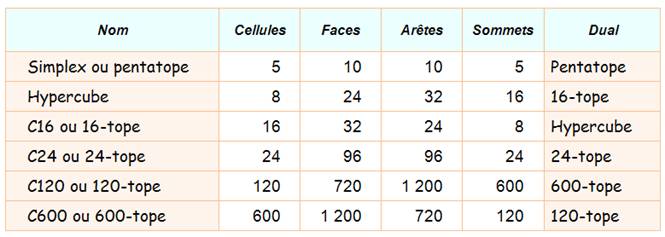
Les six POLYTOPES RÉGULIERS

 

Voir Simplexe

*      Pour les polytopes, la Relation d'Euler s'écrit:

 

Sommets + Faces = Arêtes + Cellules

 

 

 

  

AUTRES POLYTOPES

 

Dimensions supérieures (à 4)

 

*      En dimension cinq ou plus, il n'existe que trois polytopes convexes réguliers.

 

Polytope spécial

 

*      Représentation du groupe de Lie E8

 

Familles de polytopes

 

*      Voici un récapitulatif des plus simples d'entre eux:

 

 Suite en Liste des polytopes

 

*      La famille comporte les sous-familles des simplexes réguliers, famille généralisant la notion de triangle (D2) et du tétraèdre (D3); en D4, nous aurons le pentachore.
Un simplexe est l'enveloppe convexe d'un ensemble de (n+1) points. Son nom vient du fait qu'il s'agit de l'objet clos le plus simple enveloppant un groupe de points donnés.


Par exemple, un simplexe de dimension 5 (D5), aussi nommé hexatère,  possède: 6 sommets, 15 arêtes, 20 faces triangles, 15 cellules tétraédriques et 6 "faces" pentachores. L'hexatère est l'un des 19 polytères uniformes.



*      Selon la dimension, ces objets prennent effectivement des noms dont la racine est issue du grec:

 

*      Les polytopes sont une source inépuisable de découvertes. Je vous laisse  les découvrir sur Internet. Laissez-vous guider sur Wikipédia français et également anglais.

 

 

 

 

 

Suite

*    Tectoèdres

*    Hypercube

*    Hypersphère

*    Quatrième dimension

*    Parallélotope

*    Permutoèdre

Voir

*    Constructions

*    Géométrie – Index

*    Illusions d'optique

*    Polyèdres

*    Radian

*    Triangles

*    Vocabulaire de la géométrie

DicoNombre

*    Nombre 6

Sites

*    Hyperspace Star Polytope Slicer (animation)

*    Polytopes réguliers – Liste

*    Polytope Movie Page

*    Polytopes

*    Polytopes – Noms

*    Uniform Polytopes

Cette page

http://villemin.gerard.free.fr/Wwwgvmm/Geometri/Polytope.htm