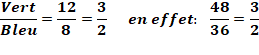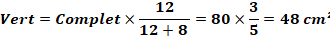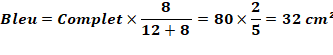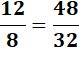|
||||||||||||||||||||||||||||
![]()
|
BIENVENUE en particulier AUX PROFESSEURS ET ÉLÈVES DES ÉCOLES ET LYCÉES En
effet: cette page est liée à un site qui vous est dédié: NOE-éducation
|
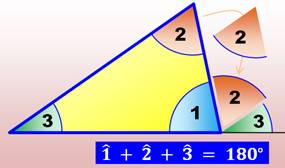
Si les triangles avaient un Dieu, ils lui donneraient trois
cotés. Montesquieu Voir Pensées
& humour Perle mathématique: Le
triangle est un rectangle avec
un côté en moins. |
|
|
||
|
Figure
géométrique
à trois
côtés Polygone à trois côtés. Figure
constituée de trois points non alignés, appelés sommets du triangle. Étymologie: latin triangulum, de tres, trois, et angulum,
angle.
|
|
|
|
Le
triangle à
|
||
|
|
||
|
Trilatère: trois droites ne
formant pas un faisceau. |
Trois
droites a, b, c sont en faisceau lorsqu'il existe une droite d telle qu'une
réflexion par rapport à d est égale à une combinaison des réflexions par
rapport à a, b et c
|
|
** Notion avancée
|
TYPES de TRIANGLES |
|
|
|
Général |
|
|
|
Selon
les angles |
|
|
|
Selon
les côtés |
(45° pour le triangle isocèle
et rectangle)
|
|
|
Et
bien d'autres |
Pédal
/ Orthique / Orthocentrique Harmonique d'un quadrilatère Calabi
/ Hellbronn /
Sierpinski Curviligne
/ Sphérique /
Etc. |
|
Suite et développements >>>
|
Autres
triangles non-géométriques |
Voir aussi Expression
avec le mot "triangle" |
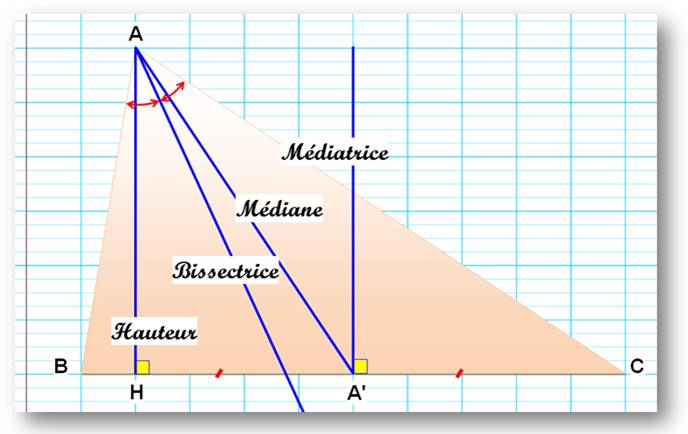
Les
quatre droites remarquables du triangle (12 au total)
|
|
||
|
HYPOTÉNUSE CATHÈTE BASE |
|
|
|
CÉVIENNE MÉDIANE HAUTEUR BISSECTRICE |
|
|
|
MÉDIATRICE |
|
|
|
BROCART |
|
|
|
|
Suite
et développements >>> |
|
|
|
||
|
Triangle |
|
|
|
Angles |
|
|
|
|
|
|
|
Côtés
et angles |
|
|
|
Triangles |
|
|
Similitude |
Ce
sont les trois cas d'égalité des
triangles >>>
Ce
sont les trois cas de similitude des
triangles. Voir Développements / Exemple / Dans le cercle
/ Théorème
de Thalès |
|
Céviennes |
|
|
Périmètre |
|
|
|
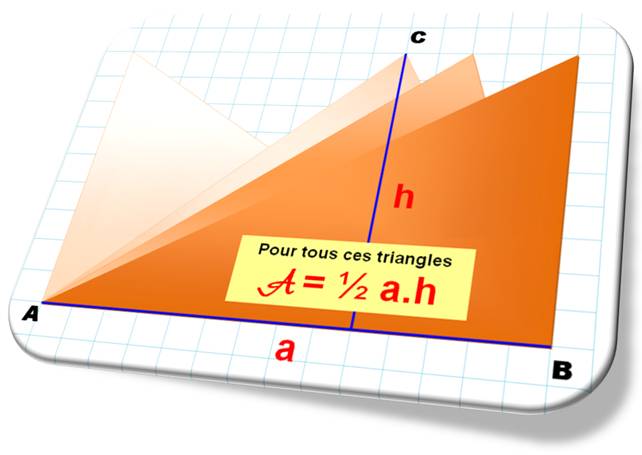
(opposé
au sommet dont la hauteur est issue) pour
le triangle quelconque.
pour
le triangle rectangle.
formule de Héron, tout
triangle (s est le demi-périmètre).
pour
le triangle équilatéral. Voir Illustrations ci-dessous |
|
Cercles |
|
|
|
|
|
Voir Aire du
triangle par méthodes analytiques
|
|
Suite Médianes du triangle / Relations métriques dans le
triangle /
Bissection du triangle / Découpe du triangle en 7
|
|
||
|
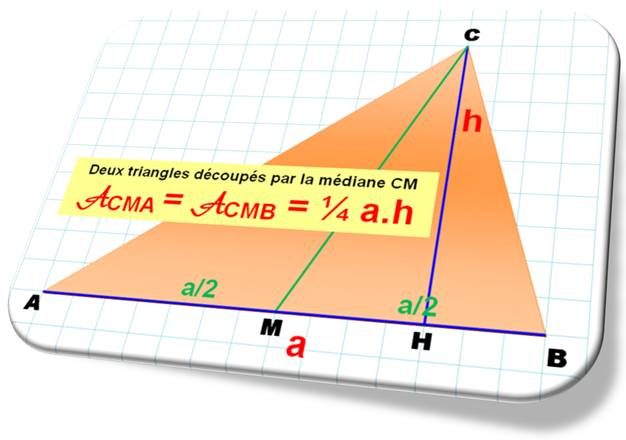
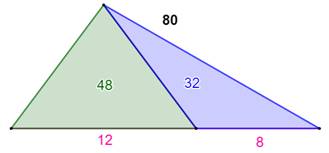
Propriété: proportionnalité Un segment, dit cévienne, découpe le triangle quelconque en deux triangles:
vert et bleu. Les aires de ces triangles sont proportionnelles aux longueurs des
segments découpés sur le côté du triangle. Aires des deux triangles Connaissant l'aire du triangle complet et les longueurs découpées, on calcule l'aire du triangle
vert et celle du triangle bleu:
|
Pour toute cévienne dans un triangle quelconque
|
|
Voir Aires proportionnelles – Brève
61-1208
|
|
||
|
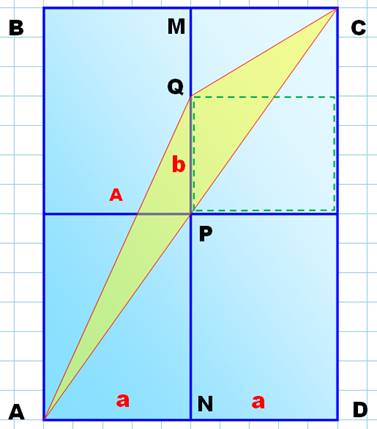
Ces deux aires sont égales.
|
Aire triangle
jaune = aire rectangle pointillé vert |
|
Voir Application au calcul du segment de
parabole
Merci à Christina T.
|
|
|||||||||||||||||||||||||||||||||
Voir le DicoNombre |
|||||||||||||||||||||||||||||||||
|
|
||
|
|
|
|
![]()
|
Suite |
|
|
Aussi |
|
|
Sites |
|
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/Geometri/Triangle.htm |
![]()