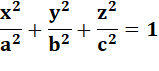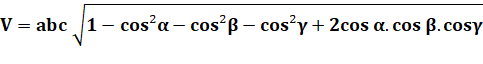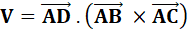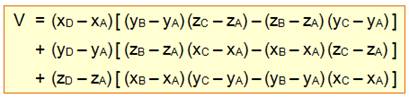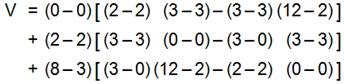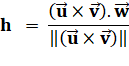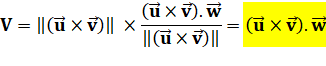|
||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
Pavé ou Parallélépipède Définition,
propriétés et amusements. Parfois aussi nommé: brique.
|
|
Anglais: Parallelepiped or rhomboid / Vertex, face and edge /Length,
breadth and height / Face diagonal and space diagonal >>>
Étymologie: Du latin:
parallelepipĕdum; issu du grec ancien: parallêlônepipedon, qui a des plans
parallèles.
Parallelos (parallèle) et epipedon (une surface
plane. De epi, sur et pedon, le sol.
|
|
|||
|
Pavé quelconque Volume
dont les six faces sont des parallélogrammes
Les faces
opposées sont parallèles et congruentes (égales). Les
arêtes sont de même longueur quatre à quatre. Comme
tous les polyèdres, le pavé vérifie la formule
d'Euler (invariant égal à 2): S + F – A = 8 + 6 – 12 = 2
Anglais: parallelepiped or rhomboid |
La somme des angles à un sommet n'excède jamais 360°; cas où une arête
est tellement oblique qu'elle tend à appartenir au plan formé par les deux
autres. |
||
|
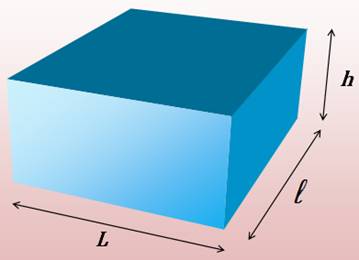
Les trois
dimensions sont:
|
Il suffit de définir trois vecteurs
avec ces trois dimensions (normes) pour définir un parallélépipède quelconque. Le sommet opposé à l'origine des trois vecteurs
représente la somme
des trois vecteurs dans l'espace. La multiplicité des chemins pour
rejoindre ces deux points montrent que la somme des vecteurs et commutative
et associative. Voir Calcul (vectoriel) du volume |
||
Voir Parallélépipède
quelconque, mais parfait / Rhomboèdre, pavé avec
faces en losanges
|
|
|||
|
Pavé droit ou parallélépipède
rectangle (ou prisme carré droit ou brique) Pavé dont
les six faces sont des rectangles. Chaque
face a quatre angles droits. À chaque
sommet, le trièdre est composé de trois angles droits. Anglais: rectangular cuboid |
|
||
|
Formules Périmètre
= somme des longueurs des arêtes. Une
grande diagonale
relie deux sommets opposés du pavé:
|
|
||
|
Faces
opposées Bases Aire
totale Aire
latérale |
Faces qui n'ont aucune arête en commun Les deux faces de plus grandes dimensions Aire des six faces Aire des quatre faces hors les bases |
||
|
|
||
|
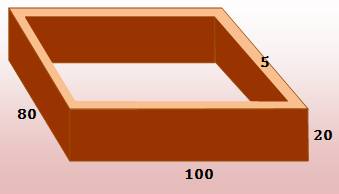
Quelle quantité de béton
pour remplir ce coffrage? Solution en partant du volume évidé Volume du parallélépipède
extérieur: Ve = 100 x 80 x
20 = 160 000 cm3 Volume intérieur (attention
deux fois l'épaisseur!): Vi = (100 – 2x5)
x (80 – 2x5) x 20 = 126 000 cm3 Volume du coffrage: Vc = Ve
– Vi = 160 000 – 126 000 =
34 000 cm3 Solution des quatre panneaux Volume des panneaux avant et
arrière: V1 = 2 x (100 –
5) x 20 x 5 = 19 000 cm3 Volume des panneaux
latéraux: V2 = 2 x (80 –
5) x 20 x 5 = 15 000 cm3 Volume total: V1 + V2
= 19 000 + 15 000 = 34 000 cm3 |
Dimensions en cm |
|
Merci à Christian
T.
|
|
|||
|
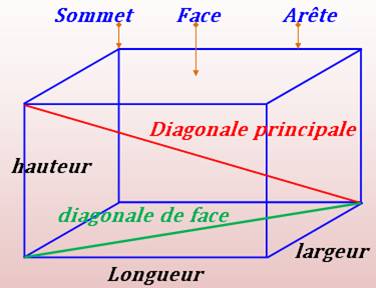
Diagonales de la face d² = L² + l² = 100 +
25 => d = 11,18… Il y en a
douze (2 par face) en trois groupes de 4 de
même longueur. Diagonales principale ou grandes
diagonales D² = d² + h² = L² + l² + h² = 100 +
25 + 49 = 174 => D = 13,19… Il y en a
quatre, toutes de même longueur et
concourantes. Anglais: face diagonal & space diagonal |
|
||
|
Règle du parallélépipède Dans
un parallélépipède quelconque, les grandes
diagonales sont concourantes et le point d'intersection les bissecte. La somme de leur carré est égale à la somme des
carrés des douze arêtes. |
Dans
le pavé droit, les quatre grandes diagonales sont de même
longueur. |
||
|
|
|
|
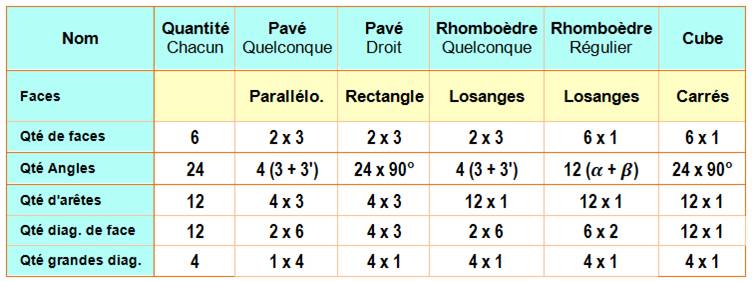
Famille Le pavé
peut être quelconque (faces parallélogrammes) ou droit (faces rectangles). Avec des
faces en losanges, c'est un rhomboèdre qui devient
régulier si tous les losanges sont identiques, mais dans tous les cas toutes
les arêtes sont de même longueurs. Avec des
faces carrées, le pavé devient cube. Nomenclature
Cousinage Parallélépipède:
famille des zonoèdres =
polyèdre
à six faces (hexaèdre) dont les faces sont
parallèles
deux à deux; =
prisme dont la base est un parallélogramme; =
parallélotope de dimension 3. |
|
Voir Parallélogramme
et sa famille / Brique
parfaite / Filiation des rhomboèdres
|
|
||
|
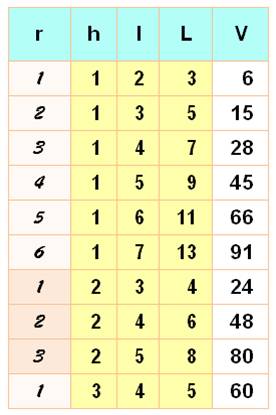
Énigme Quels
sont tous les pavés dont les dimensions sont en progression
arithmétique et qui ont un volume inferieur à 100. |
Formulation h est la plus
petite dimension et r est la raison de la progression arithmétique
(le terme constant à ajouter). Alors: V = h . (h
+ r) . (h
+ 2r) < 100 |
|
|
Résolution Une
simple exploration va permettre de résoudre cette énigme. On exclut
le cas trivial d'une raison nulle comme 2 x 2 x 2 = 8. Solutions Avec V
< 101, il y a dix possibilités avec
un volume maximum pour 1 x 7 x 13 = 91 Avec V
< 1001, il y a 69 possibilités
avec un volume maximum atteint pour 9 x 10 x 11 = 990. Avec V
< 10 001, il y a 374 possibilités
avec un volume maximum atteint pour 10 x 25 x 40
= 10 000 ou 10 x 10 x 10 pour la solution triviale. Avec V
< 100 001, il y a 1 917
possibilités avec un volume maximum atteint pour 30 x 49 x 68 = 99 960. |
Les 10 pavés dont les dimensions
sont en progression arithmétique et dont le volume n'excède pas 100.
|
|
Voir Énigmes – Index
À la base une énigme célèbre et déroutante
|
Énigme des trois filles Un dialogue succinct entre deux personnes et
l'âge des trois filles peut être déterminé. Énigme résolue du fait de la propriété singulière du nombre 36. |
Nombre 36 Deux triplets de nombres (des diviseurs de 36)
ont même somme (S) et même produit (P).
|
|
Construction avec ces triplets Deux parallélépipèdes ayant
* somme des périmètres des quatre faces (et non
longueur des 12 arêtes). |
|
Voir Nombre 36 / Nombres recenseurs / Brève 63-1243
|
|
||
|
Source
image: Ellipsoid – Wikipedia |
Équation de l'ellipsoïde
avec a < b < c, les demi-axes principaux de
l'ellipsoïde. |
|
|
Le plus
grand parallélépipède inscrit dans un ellipsoïde a pour volume: |
|
|
Voir Ellipse
|
|
||
|
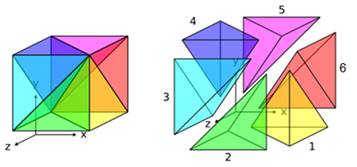
Théorème Prenons
le tétraèdre formé par trois arêtes issues du
même sommet; son volume est égal à un sixième de celui du parallélépipède. English:
The volume of any tetrahedron that shares three converging edges of a
parallelepiped has a volume equal to one sixth of the volume of that
parallelepiped.
Source
image: Dune |
|
|
|
Les quatre types de tétraèdres
inscrits dans un parallélépipède
|
||
Voir Dissection
du cube en tétraèdres
|
|
||
|
On connait la longueur des 3 côtés
et les angles entre ses trois cotés
|
||
|
On connait les coordonnées des
trois vecteurs
Voir Justification Traduction en coordonnées
Le volume
de chacun des tétraèdres est égal à 1/6 de cette valeur. |
|
|
|
Exemple simple
= 0 + 0 +
5 [3 x 10 – 0] = 5 x 3 x 10 Ce qui
est bien la formule classique du volume du parallélépipède rectangle. |
|
|
|
|
||
|
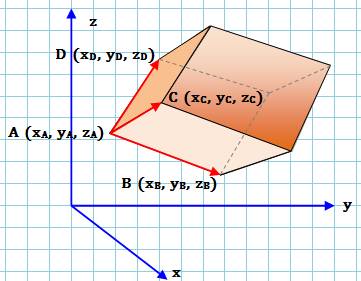
Un
parallélépipède défini par les trois vecteurs u, v et w. Le
produit vectoriel
(x) de u et v produit un vecteur orthogonal au plan contenant u et v. Sa norme (longueur) est égale à l'aire du parallélogramme (= u . v .
sin bêta et v . sin bêta est une hauteur). Le
produit scalaire
(.) entre ce nouveau vecteur et w fait intervenir l'angle alpha. Or
longueur de w x cos alpha est la hauteur (h) du parallélépipède, celle qui
permet de calculer le volume de ce solide. |
|
|
|
Valeur
d'alpha (trigonométrie). |
|
|
|
Valeur
d'alpha (vectoriel: produit scalaire) Avec A =
(u x v) et B = w. |
|
|
|
En
égalant: |
|
|
|
Volume =
aire de la base x hauteur. Trois
formules sont possibles en choisissant l'une des trois faces comme base. |
|
|
|
Calcul de
l'angle alpha avec le volume divise par le produit des trois longueurs
d'arêtes. |
|
|
|
|
||
|
Parallelepiped |
Parallelepiped is a prism, bases of which are parallelograms. So, a
parallelepiped has six faces and all of them are parallelograms. Opposite
faces are two by two equal and parallel. A parallelepiped has four space diagonals; they all intersect in the one
point and they are divided into two equal parts. |
|
![]()
|
Suite |
|
|
Aussi |
|
|
DicoNombre |
|
|
Sites |
|
|
Cette page |
![]()