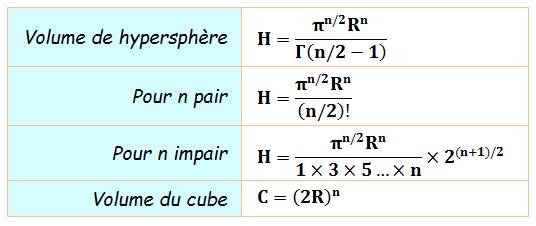|
||||||||||||||||||||||||||
![]()
|
HYPERCUBE
ou
TESSÉRACT ou 4-Cube ou Octachoron L'hypercube est l'un des six polytopes
réguliers convexes. Un pionner de la quatrième dimension
et de l'hypercube: Charles
Hinton |
Voir Quatrième
dimension
|
|
||||
Voir Explications
|
||||
|
Le cube est le volume engendré par un simple carré que
l'on déplace en ligne droite (translation). On peut le représenter en dessinant le carré au
départ et le carré à l'arrivée et
joindre les quatre sommets.
Un cube en se translatant engendre un hypercube. |
|
|||
|
un petit à l'intérieur d'un plus grand, les sommets de l'un étant réunis aux sommets de l'autre. L'hypercube comprend 8 cubes. Ce sont le cube de départ, les six
cubes créés à partir des six faces et le cube qui semble englober l'ensemble.
Ou plus justement, un cube se projette sous la forme de
deux carrés, l'un dans l'autre.
Cette figure est la représentation que nous pouvons nous
en faire dans notre monde à 3 dimensions, et encore, lorsqu'on le dessine,
projeté sur 2. |
Voir
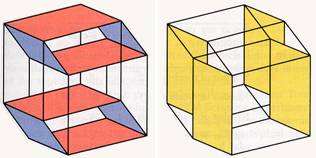
Grande Arche Chaque cube (bleu et rouge) compte
12 arêtes. En y ajoutant les 8 arêtes (bleues) les reliant, on obtient les 32
arêtes de l'hypercube. Faces planes Identification de 3 x 4 faces
En faisant la même figure avec les
faces verticales à gauche et horizontales à droite, Il y en encore 3 x 4 faces. Soit un total de 24 faces planes. |
|
Que devient l'hyper cube ? Huit cubes, 4 en lignes et 4 autour du deuxième. Il n'y a pas de cube central.
|
Cellules cubiques (cell or 3-face, en anglais) Cette figure montre les 8 cellules
ou faces de forme cubique. |
|
Source image
Wikipédia
et La Recherche n°513-514 Wikipédia
présente les projections pour les dimensions 2 à 12 |
|
La Grande Arche de la Défense à Paris
|
|
(1) En forme d'un grand cube
évidé par un plus petit cube, elle
fait penser à la vision 3D d'un hypercube. (2) Cette partie suspendue
est notamment utilisée pour des réceptions (J'y suis allé plusieurs fois. Impressionnant!). (3) Le nuage est destiné à
briser la monotonie de la rectitude de l'Arche (Mon oncle en a calculé les composantes). (4) Le parvis donnant sur de
nombreuses tours d'affaires fut un lieu de passage fréquent pour moi. |
Dali et la croix du Christ en hypercube
|
Corpus hypercubus est un tableau peint en 1954 par Salvador
Dalí ; il représente Jésus crucifié sur le patron tridimensionnel d’un
tesseract. Gala, l’épouse de Dalí, y est représentée en une Vierge
Marie contemporaine, qui contemple Jésus crucifié. En arrière-plan, la baie de Portlligat. Le tableau est au Metropolitan Museum of Art de New York. |
|
Voir Constructions
/ Arche et invariant d'Euler
![]()
|
|
|
|
Le globe (3D) projeté sur un plan donne un cercle,
l'hémisphère proche de la source lumineuse et l'autre se confondent dans leur
projection sur le plan.
sous la forme de deux sphères intimement mêlées. Ce serait comme deux pommes l'une dans l'autre, telles
que leurs peaux se rejoignent.
Elle ne peut être obtenue qu'en exerçant une rotation
dans la quatrième dimension à partir de vous même. Comme dans le cas de vos mains dans un pays plat à deux
dimensions. La main droite pour devenir votre main gauche doit subir
une rotation dans la troisième dimension. Une simple rotation dans le plat pays n'y suffit pas. On peut comparer l'opération miroir sur votre corps à
celle d'un gant que l'on retourne. Brrr. Volume de l'hypersphère de dimension n
Voir Fonction
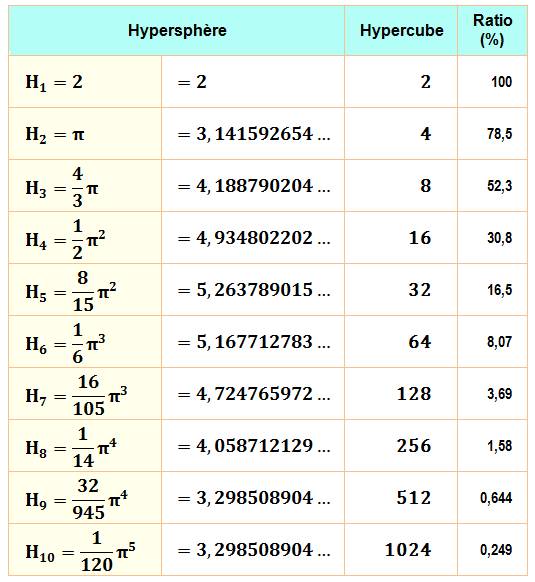
GAMMA ( Valeurs pour les dimensions 1 à 10 et un rayon unité
Volume maximum pour n = 5. Pour tendant vers l'infini, le
volume tend vers 0. L'hypersphère occupe de moins en moins l'espace de son
hypercube circonscrit lorsque n augmente. Notez la valeur proche de 50% pour la sphère ordinaire. |
|
Voir Empilement
des sphères et hypersphères
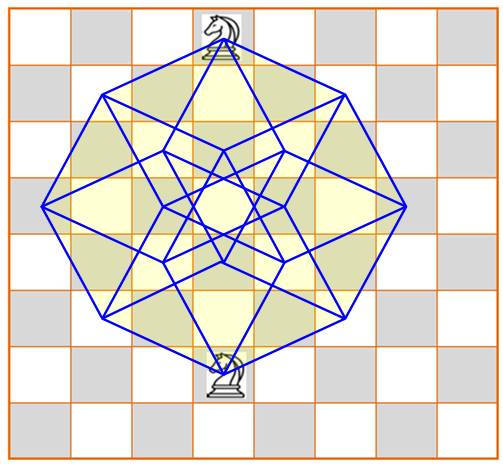
Les 24 (= 4!) trajets possibles
du cavalier pour rejoindre la position six cases plus bas
C'est la représentation de l'hypercube
![]()
|
Suite |
||
|
Voir |
||
|
DicoNombre |
|
|
|
Site |
|
|
|
Cette
page |
||
![]()