|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Mono: une bille
est plus lourde (ou plus légère) Ambi: une
bille est plus lourde ou plus légère
sans que nous le sachions a priori |
![]()
|
Énigme de la pesée impossible des DOUZE BALLES Compléments Page complémentaire montrant
une variante de la résolution de cette énigme avec
les notations telles que je les avais imaginées il y a une bonne trentaine
d'années. Plus quelques informations
complémentaires. |
|
|
||
|
Intérêt historique. Voir plutôt les deux méthodes par dichotomie ou par combinaisons. La méthode ci-dessous est une variante de la méthode par
dichotomie qui utilise autant que possible la connaissance des boules neutres
(standard) déjà identifiées. |
||
|
Problème On dispose de douze
boules de billard.
En trois pesées sur
une balance à plateau, sans poids, retrouver cette boule et dire si elle est
plus lourde ou plus légère. Voir Un million de balles |
Commentaires Ce
problème semble anodin, puis, en y réfléchissant un peu, semble totalement
infaisable. Il a alimenté de nombreux salons où le sujet principal consistait
surtout en la possibilité de le résoudre. Il existe
une manière de procéder pour éviter des recherches vite foisonnantes. Elle
repose sur la comparaison du nombre de possibilités pour les boules au nombre
de conclusions que l'on peut tirer des pesées restantes. Voici la
solution, mais d'abord commençons par une familiarisation avec le type de
conclusions tirées d'une pesée. |
|
|
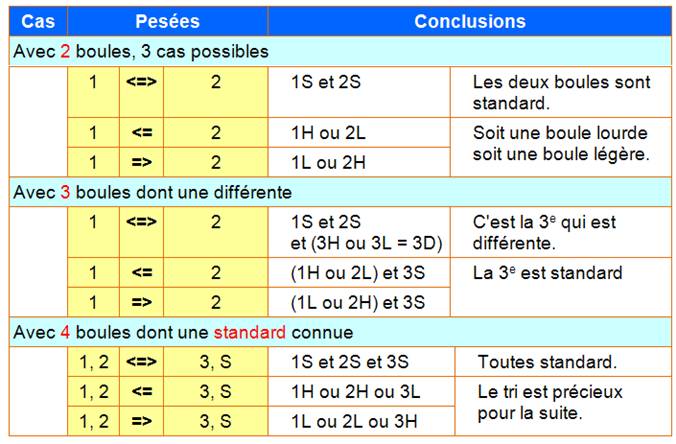
Notations
|
||
![]()
|
Principe de base
|
|
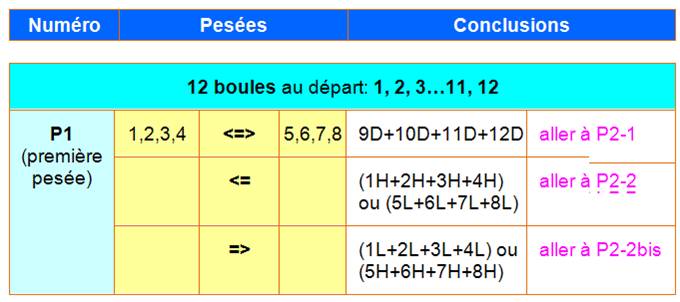
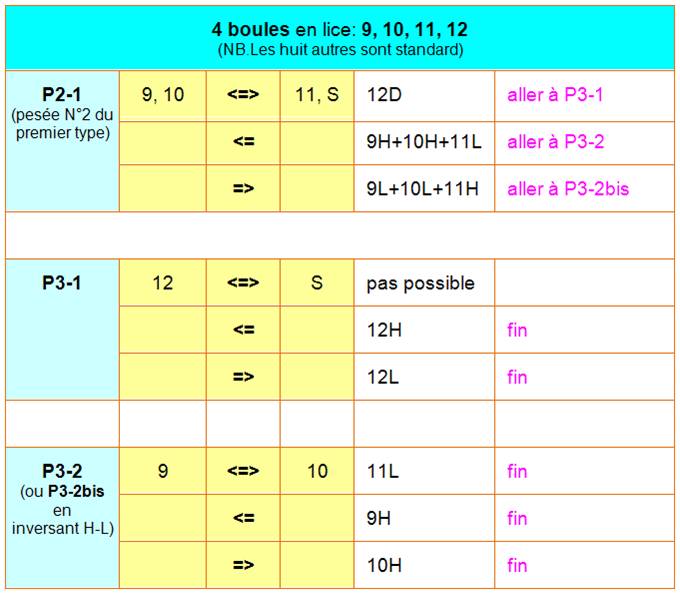
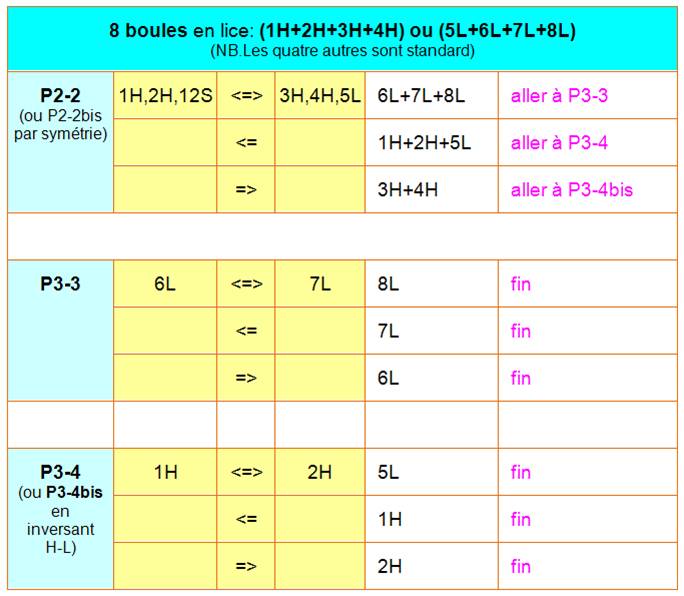
Solution en trois
pesées P1, P2 et P3
Lecture de la première
ligne
Pour la suite des
pesées, se reporter plus pas au numéro P2-1.
Pour la suite des
pesées, se reporter plus pas au numéro P2-2. |
![]()
|
|
|
|
![]()
|
Retour |
|
|
|
|
|
Voir |
|
|
DicoNombre |
|
|
Sites |
Voir
liste |
|
Cette
page |
![]()