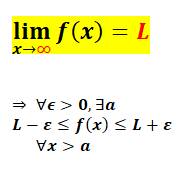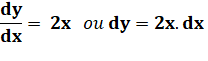|
|||||||||||||||||||||||||||||||||||||||||||||
![]()
Humour
|
On appelle
spécialiste quelqu'un qui sait de plus en plus de chose sur un sujet de moins
en moins étendu. À la limite, le
spécialiste sait tout … sur rien. Michel Chrestien |
Voir Pensées & humour
|
LIMITES de Fonctions La notion de limite est intuitive: par exemple, x² tend vers l'infini lorsque x est de plus en plus grand. À leur habitude, les mathématiciens ont apporté plus de précision à cette notion de manière à la traiter en véritables objets mathématiques. On parlera de limite ou de convergence.
|
|
|
||
|
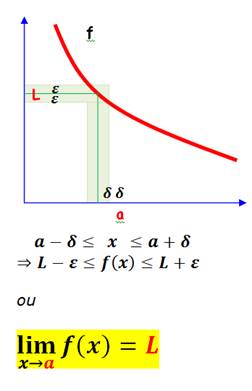
Fonction
finie
On peut rendre
f(x) aussi proche de L que l'on veut, sur un intervalle aussi petit
soit-il autour de a. |
|
|
|
Fonction
infinie
On peut rendre
f(x) aussi proche de Note: idem pour moins l'infini. |
|
|
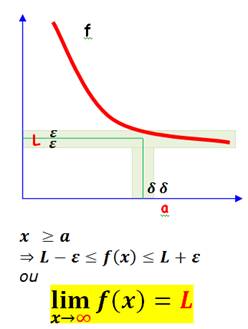
Fonction
limitée
On peut rendre
f(x) aussi proche de L que l'on veut, au-delà d'un seuil a aussi grand
soit-il. Note: idem pour moins l'infini. |
|
|
Autre formulation de la définition
|
|
|
|
||
|
dy = (x + dx)² – x² = x² +
2x.dx + dx² – x² =
2x.dx + dx²
dy = 2x.dx |
|
|
Humour

![]()
|
Suite |
|
|
Voir |
|
|
Aussi |
|
|
Cette page |
http://villemin.gerard.free.fr/aMaths/Analyse/Limite/Defini.htm
|
![]()