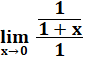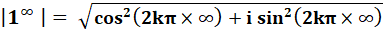|
|||||||||||||||||||||||||||||||||||||||||||||
![]()
|
1INFINI
|
Voir Zéro, un et infini
|
|
||
|
|
1 x 1 = 1 1 x 1 x 1 = 1 1 x 1 x … x 1 = 1 1 x 1 x … = ? |
|
|
|
Il nous faut
une fonction proche de 1; alors 1 plus un chouia? Pourquoi pas?
Comment se
comporte cette fonction à la puissance infinie ? Sachant que lorsque
x tend vers 0, l'expression est celle qui nous occupe. |
|
|
|
Comment se
comporte cette fonction lorsque x tend vers 0 ? |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
ln L = 1 L = e |
|
|
|
X f(x) 1/10 2,5 1/100 2,70 1/1000 2,716 1/10000 2,7181 1/100000 2,71826 e = 2,718281828 |
|
Voir Explications complémentaires
|
|
||
|
|
1 x 1 x … x 1 = 1
Indéterminé Note: les logiciels de calcul donnent cependant la valeur 1. > limit(1^x,x=infinity); 1 |
|
|
Comparaison?
|
|
|
||||
|
Intervalle |
Valeur |
Exemple x
petit |
Exemple x
grand |
|
|
0 < x < 1 |
|
0,1100 = 10 – 100 0,1 – 100 = 10 100 |
0,9100 = 0,000026… 0,9 – 100 = 37 648, 6… |
|
|
1 < x < |
|
2100 = 1, 26… 1030 2 – 100 = 7,888…10 – 31 |
100100 = 100200 100 – 100 = 10 – 200 |
|
|
x = 1 |
|
La part réelle et la part imaginaires sont indéterminées. Mais le module est égal à 1. |
||
|
À partir de cette
valeur => |
|
|||
|
Portée à la puissance infinie |
Ces deux valeurs, en cosinus et sinus d'un angle infini, sont
indéterminées. En effet, impossible de fixer un point sur le cercle
trigonométrique correspondant à un angle infini. |
|||
|
Calcul du module |
|
|||
![]()
|
Suite |
|
|
Voir |
|
|
Aussi |
|
|
Cette page |
http://villemin.gerard.free.fr/aMaths/Analyse/Limite/UnPinfin.htm
|
![]()