NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 22/09/2023 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	ANALYSE
Débutants Général	Dérivées				Glossaire Dérivée
INDEX Analyse	Approche	Historique	Débutants	Développement
	Ficelles de première		Approche en première	Les dérivées usuelles
	Intérêt des dérivées		Exemples résolus	Exemples (limites)
	Pente		Exemples en trigo	Problème du sofa
	Lycée		Sommaire de cette page >>> Approche de Newton >>> Contestation >>> Approche moderne

DÉRIVÉES

Comment caractériser, mesurer la variation d'un phénomène?

Comment calculer la tangente en un point d'une courbe?

Comment approcher l'infiniment petit?

Anglais : Derivate

APPROCHE de NEWTON qu'il appelait méthode des fluxions Calcul Simple et efficace
Newton considérait une fonction ou, pour nous simplifier la vie ici.	y = ax² + bx + c y = x² + x + c
Il imaginait l'évolution de la fonction selon que le temps s'écoulait. Pour percevoir le détail local, il prenait un tout petit intervalle de temps.	qu'il notait o
Il imaginait que x changeait d'une toute petite quantité durant ce temps.	ox' selon sa notation, il ajoutait un point sur le x ; je mets un prime (plus facile à faire).
Il s'intéressait à ce que devenait alors y pendant ce même petit intervalle de temps.	oy'
La fonction, au bout de cet intervalle de temps devient:	y + oy' = (x + ox')² + (x + ox') + c
En calculant En organisant En enlevant y de chaque côté	y + oy' = x² + 2x(ox') + (ox')² + x + ox' + c y + oy' = x² + x + c + 2x(ox') + (ox')² + ox' oy' = 2x(ox') + (ox')² + ox'
Newton ayant fait l'hypothèse que ox' est vraiment tout petit. C'est encore plus vrai pour son carré (ox')². Il est quasi-nul et peut-être ignoré, négligé. Et, après mise en facteur:	oy' = 2x(ox') + ox' + (ox')² oy' = 2x(ox') + ox' oy' = (2x + 1) ox'
Il obtient ainsi la pente de la courbe. Et jugeant que l'intervalle de temps n'est plus nécessaire; il note:	oy'/ox' = 2x + 1 y' / x' = 2x + 1
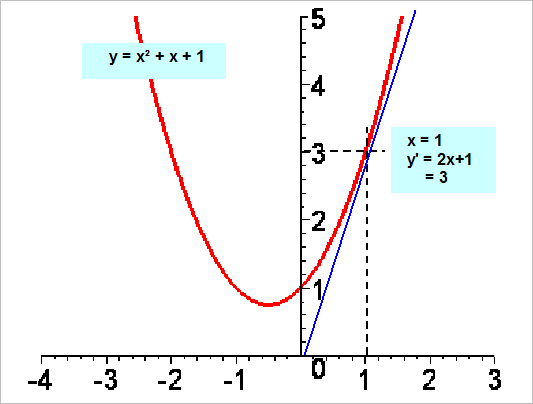
Ou, autrement dit, le coefficient directeur de la tangente en tout point de la courbe en x = 0 en x = 1	En x = 0 =>pente = 1 En x = 1 =>pente = 3 (voir illustration)

Illustration

Citation

La dérivée selon Newton :

Le quotient ultime de deux accroissements évanescents.

Voir Pensées et Humour

CONTESTATION

Il se trouve que cette méthode est efficace. Elle donne les bons résultats pour le calcul des tangentes (dérivation); comme celui des superficies (intégration). Mais, certains contestaient le manque de rigueur du raisonnement. Dire que (ox)² est quantité négligeable donc nulle et on la supprime, cela dérangeait les mathématiciens de l'époque. Newton affirmait que si (ox)² est égal à 0 alors, c'est que ox lui-même était nul. Les contestataires avaient beau jeu de démolir la méthode en disant qu'il est interdit de diviser par 0, on ne sait plus ce qu'on fait …

APPROCHE MODERNE
On définit la dérivée comme une limite. se lit epsilon.	f'(x) = limite de { f(x + ) – f(x) } / lorsque tend vers 0
En reprenant l'exemple Et pour y' = f ' (x) En calculant En effectuant les opérations	y = x² + x + c y' = { (x + )² + x + + c – (x² + x + c) } / e y' = { x² + 2x + ² + x + + c – x² – x – c } / y' = { 2x + ² + } /
Soit le résultat	y' = (2x + ² + ) /
On se souvient que tend vers 0, il n'est cependant pas nul On peut diviser par Soit le résultat	y' = 2x + + 1 y' = 2x + 1 +
Maintenant, nous pouvons nous exprimer en terme de limite.	y' = limite de 2x + 1 pour

Bilan

Le truc du petit intervalle de temps a permis à Newton de trouver la méthode de calcul.

L'astuce de la limite fut précieuse pour mettre tous les esprits en paix.

Désormais, les calculs de différentiation et d'intégration sont couramment utilisés pour résoudre de nombreux problèmes de physique.

Quand x² devient 2x

Sur un bateau x² est à barre quand soudain, il rencontre un fort courant. Sauriez-vous combien ils sont à bord? Deux x, car le bateau dérive.

Voir Pensées & humour

Suite	Application au calcul du volume maximum d'une boîte Application au passage du sofa dans un couloir Brève 243 – Calcul différentiel et intégral Calcul du chemin optimum Calcul par intégrales Intégrales Primitives Dérivées – Glossaire Dérivées – Historique Équations différentielles – Glossaire Les 17 équations qui ont changé le monde Rayon de courbure et calculs de dérivées
Voir	Analyse – Glossaire Champs Équations différentielles Équations de Navier-Stokes Équations de Schrödinger Exponentielles Exposants – Index Limites Logarithmes Opérateur hamiltonien Opérateur laplacien Vitesse – Glossaire
Livre	Méthod'S mathématiques Terminale S – Bruno Clément – ellipses – 2012
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Analyse/AnaDeriv.htm