|
Édition du: 16/04/2023 |
|
INDEX Nombres
(Classification) |
NOMBRES CHANCEUX |
|||
![]()
|
Problème de Josèphe ou de Josephus Vieux
problème qu’aurait rapporté l’historien Flavius Josèphe (Ier
siècle de notre ère) où il s’agissait, dans un cercle de soldats prisonniers,
d’en éliminer un sur trois. Le
problème de Josephus, un procédé de tri sélectif, est un classique en matière d'exercice de programmation. Objet également de nombreuses variantes au cours de l'histoire. On
commence par les nombres chanceux de Josèphe résultant de l'application d'un
crible très simple. |
||
|
|
Sommaire de cette page >>> Nombres chanceux de Josèphe >>> Texte original >>> La légende de Josephus >>> Le problème de Joseph >>> Théorie – Passage en binaire >>> Programmation >>> Exemple avec k = 3 |
Débutants Glossaire |
|
Nombres qui résistent
au crible de tri sélectif simple suivant: On commence par lister les nombres entiers et on
en élimine un sur deux; restent les
nombres impairs sur la deuxième ligne. Parmi ceux-ci, on en élimine un sur trois. Parmi ceux qui subsistent, on en élimine un sur quatre, etc. Les nombres chanceux d'Ulam sont engendrés
par un procédé voisin. |
|
|
|
Sur ce tableau en colonne de
gauche, le numéro de la ligne k qui indique qu'un nombre sur k est éliminé. Le premier tri élimine les nombres pairs. Ils ne
sont pas représentés sur ce tableau. En jaune, les nombres éliminés.
|
||
|
Suite des nombres chanceux de
Josèphe jusqu'à 5 000 1, 3, 7, 13, 19,
27, 39, 49, 63, 79, 91, 109, 133, 147, 181,
207, 223, 253, 289, 307,
349, 387, 399, 459, 481, 529, 567, 613, 649, 709, 763,
807, 843, 927, 949, 1009, 1093, 1111, 1189,
1261, 1321, 1359, 1471,
1483, 1579, 1693, 1719, 1807, 1899, 1933,
2023, 2161, 2187, 2269,
2367, 2479, 2533, 2703, 2739, 2799, 2967, 3019,
3147, 3199, 3327, 3421, 3529, 3619, 3807,
3841, 3913, 4083, 4203, 4249, 4407, 4603,
4623, 4783, 4891, 5067 … En rouge, les nombres premiers. L'année 2023
sera chanceuse. La prochaine dans 138 ans (2161). |
||
|
Intérêt Le mathématicien d'origine polonaise, Stanislaw
Ulam (1909-1984) a étudié ces nombres pour distinguer, parmi les propriétés
des nombres premiers, lesquelles sont la conséquence du fait qu'ils sont
issus d'un crible et lesquelles leur ont propres. |
||
Texte original de Verna Gardiner, R. Lazarus, N. Metropolis et
S.Ulam.
|
Consider the sequence of all positive integers, 1, 2, 3, … We shall
now strike out from this sequence every second term by counting from 1. The
odd integers will be left. We shall now strike out every third integer in the
remaining sequence, again starting to count from 1, but considering only the
remaining integers. We shall obtain a second sequence of integers. The next
step is to strike out every fourth integer counting only the remaining ones
and we obtain another subsequence. We can continue this process Indefinitely.
It is obvious that infinitely many integers will remain after we have
completed the process. |
Considérons la séquence de tous les nombres entiers positifs, 1, 2, 3,
... Nous allons maintenant rayer de cette séquence chaque deuxième terme en
comptant à partir de 1. Il restera les nombres entiers impairs. Nous allons
maintenant rayer tous les troisièmes entiers de la séquence restante, en
commençant à nouveau à compter à partir de 1, mais en ne considérant que les
entiers restants. Nous obtenons ainsi une deuxième séquence d'entiers.
L'étape suivante consiste à rayer chaque quatrième entier en ne comptant que
les entiers restants et nous obtenons une autre sous-séquence. Nous pouvons
continuer ce processus indéfiniment. Il est évident qu'il restera une
infinité d'entiers après que nous ayons terminé le processus. |
![]()
|
Josephus Flavius, historien
juif du premier siècle (v.34-v100). Il est prisonnier des Romains dans une cave de Yodfat (nord d'Israël actuel) avec quarante
soldats. Ceux-ci préfèrent se suicider plutôt que de se rendre. Décision est prise que chacun tuera le troisième à sa gauche et le
dernier le fera lui-même. Josephus, ne voulant pas mourir, trouva la place à occuper pour être
le dernier. Note personnelle: j'ai eu
l'occasion de visiter le site
impressionnant de Massada, une ville fortifiée perchée en haut d'un
piton rocheux. Lieu assiégé par les Romains en 72 et 73. Les occupants se
sont suicidés plutôt que de se livrer aux Romains. |
|
De nombreux experts en récréations mathématiques ont adapté le
problème de Josephus. Ainsi, Dudeney
propose un jeu de chat et de souris. Treize souris sont en cercle, toutes
noires sauf une blanche. Le chat doit manger une souris sur treize et ne
manger la blanche qu'en dernier. Par laquelle doit-il commencer. Charitable,
Dudeney explique que, le chat prenant son temps pour réfléchir s'est endormi,
et les souris se sont échappées. Le puzzle et sa solution
(anglais) Note: pour une
traduction ouvrir le site "traduction Google" ou le site
"DeepL" et copier coller le texte dans la fenêtre |
|
Le défi Ce sont cinq soldats rangés en cercle (S1, S2,
S3, S4 et S5). Ils doivent être exécutés les uns après les
autres en épargnant un soldat sur deux jusqu'à ce qu'il n'en reste qu'un
seul. L'un d'eux (le chef, un soldat méritant, ou
autre) est désigné pour être épargné. Mais, à lui de choisir la bonne place. Solution En périphérie du cercle, les nombres indiquent
l'ordre d'exécution: S2, S4, S1, S5 et S3. Le soldat en position 3 sera sauvé. On note f(5) = 3. Quelles sont les positions pour n soldats ? Voir Brève
772 |
|
|||||||||||||||||||||||||||||||||||||
|
Cas de neuf soldats Le soldat sauvé est également celui en troisième
position: f(9) = 3. |
|
|||||||||||||||||||||||||||||||||||||
|
Valeur de f(n) |
Valeur de f(n) en fonction de n (colonne colorées lorsque n = 2m)
Liste de 200 valeurs 0, 1, 1, 3, 1, 3, 5, 7, 1, 3, 5, 7, 9, 11, 13, 15,
1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23, 25, 27, 29, 31, 1, 3, 5, 7, 9, 11,
13, 15, 17, 19, 21, 23, 25, 27, 29, 31, 33, 35, 37, 39, 41, 43, 45, 47, 49,
51, 53, 55, 57, 59, 61, 63, 1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23, 25,
27, 29, 31, 33, 35, 37, 39, 41, 43, 45, 47, 49, 51, 53, 55, 57, 59, 61, 63,
65, 67, 69, 71, 73, 75, 77, 79, 81, 83, 85, 87, 89, 91, 93, 95, 97, 99, 101,
103, 105, 107, 109, 111, 113, 115, 117, 119, 121, 123, 125, 127, 1, 3, 5, 7,
9, 11, 13, 15, 17, 19, 21, 23, 25, 27, 29, 31, 33, 35, 37, 39, 41, 43, 45,
47, 49, 51, 53, 55, 57, 59, 61, 63, 65, 67, 69, 71, 73, 75, 77, 79, 81, 83,
85, 87, 89, 91, 93, 95, 97, 99, 101, 103, 105, 107, 109, 111, 113, 115, 117,
119, 121, 123, 125, 127, 129, 131, 133, 135, 137, 139, 141, 143, 145 … |
|||||||||||||||||||||||||||||||||||||
|
Propriétés |
La fonction f(n) est la suite des nombres
impairs. Elle repasse par 1 à chaque puissance de 2. |
|||||||||||||||||||||||||||||||||||||
|
Formules |
Récurrence: f(2n) = 2 f(n)
– 1 & f(2n + 1) = 2f(n) + 1 Récurrence dans le cas
général où on passe k soldats: f(n, k) = (f(n – k ) + k) mod (n) + 1 f(n, 2) = (f(n – 1 ) +
1) mod (n) + 1 f(1, k) = 0 Absolu: si n = 2m + L et 0 ≤ L ≤ 2m , alors f(n) = 2L + 1 |
|||||||||||||||||||||||||||||||||||||
|
Bit
à bit |
La solution est immédiate en binaire
avec un simple échange de bits. Exemple avec f(10) = 5
|
|
|
Amusement |
Une représentation amusante pour les valeurs de
f(n). Lire la quantité de carreaux dans la forme en
face du nombre. Ex: f(7) = 7
et il y a 7 petits carreaux dans la forme bleue en L. Représentation
due à Omar E. Pol |
|
|
Tableau du haut avec 4, 8 et 16 Si n est une puissance de 2, on vérifie que f(n) = 1. Tableau du bas avec 5, 6 et 7 Lorsqu'on ajoute un élément, f(n) progresse de 2 Formalisation Si un nombre est égal à une puissance de 2, alors f(n) = 1. Si on ajoute L à cette puissance de 2, alors on ajoute 2L à f(n) Bilan: si n = 2m + L, alors f(n) = 1 + 2L Correspondance (exemple avec valeurs binaires à droite)
|
Puissances de 2
Adjonction d'éléments
|
||||||
|
Effet binaire La puissance 2m est la
plus grande puissance de 2 incluse dans le nombre n; elle correspond au
chiffre initial de poids fort. Celui-ci contribue pour +1 dans f(n). Le nombre qui reste (n amputé du premier bit) est égal à L, lequel est
doublé pour former f(n). Or, un doublement (multiplication par 10 en binaire)
a pour effet de décaler les bits d'un cran vers la gauche. |
Bilan Le nombre binaire initial
|
|
Programme Maple avec k = 2
|
But Former la liste des valeurs
de f(n) jusqu'à une valeur spécifiée (mx). Principe Calculer les valeurs par récurrence à partir de f(0) et éditer la suite (seq). Commentaires Initialisation générale; de
la valeur de départ f(0) et de la borne de calcul (mx). Boucle de calcul avec la
formule de récurrence. Les valeurs calculées
sont conservées en mémoire avec l'étiquette f(n). En fin de programme, édition
de ces valeurs sous la forme d'une suite de valeurs . |
||
|
Programme Python avec k = 3
|
Commentaires La même formule de
récurrence est utilisée. Le calcul récursif est
implémenté par une fonction (def). Le programme principal est un
exemple: Ici, le cas historique de Josephus avec n = 41 soldats et un tué
tous les trois (k = 3). C'est le n°31 qui est sauvé. Voir
illustration ci-dessous >>> |
||
Voir Programmation – Index
|
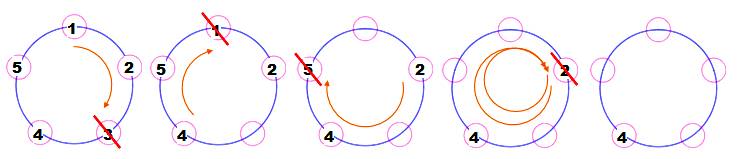
Examen détaillé du cas n = 5
et k = 3 Le cercle extérieur représente la situation au
départ. À chaque tour, les soldats épargnés avancent d'un
pas vers le centre. Les sacrifiés sont signalés par un petit carré. Au premier tour (cercle 2), les n°1 et n°2 sont
épargnés et le n°3 est sacrifié (s1). Après avoir épargné les n°4 et n°5, c'est au tour
du n°1 d'être sacrifié (s2). Etc. |
Cas n =
5, k = 3 => Sauvé en 4
|
|
|
Même cas: présentation développée en
cercles indépendants
|
||
|
|
||
![]()
|
Retour |
|
|
Voir |
|
|
Aussi |
|
|
Sites |
|
|
Cette page |
![]()