Accueil Orientation générale Barre de recherche

DicoNombre DicoMot Math DicoCulture

Atlas des maths Rubriques Index alphabétique

Nouveautés Actualités Références

Édition du: 28/03/2023 M'écrire Brèves de Maths

INDEX Graphe Topologie Dénombrement Logique Jeux	GRAPHES
	Graphes – Introduction	Arbres – Introduction	Chemin le plus court
	Chemin eulérien	Cinq pays	Voyageur de commerce
	Graphe planaire	Trois maisons	Multiple et diviseurs
	Graphe de Delaunay	Petit monde	Nombres de Delannoy
	Ivrogne	Colonies de fourmis	Nœuds
	Pont de Königsberg	Cheval	Croisements

Faites un double-clic pour un retour en haut de page

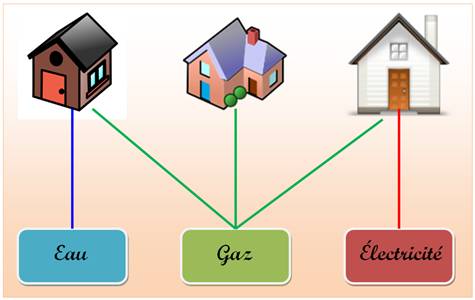
Énigme des TROIS MAISONS ou de l'eau-gaz-électricité Graphe des utilitaires (K3,3) Proposée en 1903 par Sam Loyd puis en 1917 par Henry Ernest Dudeney.
	Sommaire de cette page >>> Problème >>> Solution >>> Graphe	Débutants Dénombrement Glossaire Combinatoire

Anglais: water, gas, and electricity problem, or the (three) utilities problem, or the three cottage problem

Utility graph

Henri Dudeney (1857-1930) – Mathématicien anglais

Amateur de casse-têtes géométriques, logiques, combinatoires, passage de rivière, … Peu de formation académique, il commence sa carrière à 13 ans comme employé dans une administration anglaise. Très tôt (avant 10 ans), il s'intéresse aux problèmes d'échecs et aux puzzles. Il les publie dans le journal local. Il étudie les maths et son histoire comme loisir. Il continue à publier des énigmes sous le pseudo de "Sphinx". Il correspond avec Sam Loyd. Relation rompue lorsqu'il s'aperçoit que Loyd publie ses problèmes sous son nom.

Ses livres The Canterbury Puzzles (1907) - Les Énigmes de Canterbury (2018); Amusements in Mathematics (1917); The World's Best Word Puzzles (1925); Modern Puzzles (1926); Puzzles and Curious Problems (1931); A Puzzle-Mine; 536 Curious Problems & Puzzles (1967), annoté et préfacé par Martin Gardner, recueil contenant Modern Puzzles et Puzzles and Curious Problems. En français, 500 Casse-tête Inédits ( 2019).

Dudeney sur ces pages: Carrés magiques (historique) Chat et souris (Problème de Josèphe) Dés devinés Les cinq pièces de Dudeney Nombre 111 Nombre 2 592 Nombres de Dudeney Pavage Dissection Roméo et Juliette Somme de deux cubes rationnels

Voir Contemporains de Dudeney

Les trois maisons
Problème Comment amener l'eau, le gaz et l'électricité aux trois maisons sans que les raccordements ne se croisent? Illustration avec début de branchement Solution

SOLUTION
Il est impossible de relier ces trois maisons aux trois ressources sans croisement des raccordements. La meilleure solution ne permet de poser huit raccordements sur neuf demandés.

Graphe équivalent

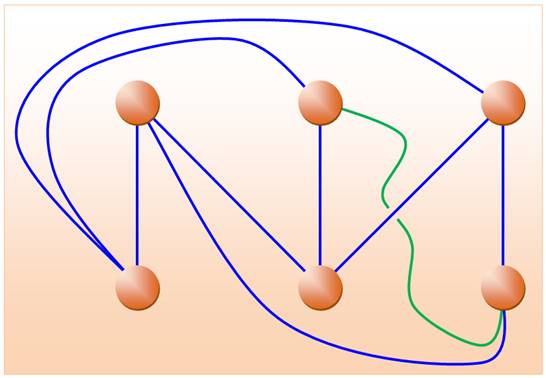
Il s'agit ici d'un problème de graphe: deux groupes de trois nœuds. Le problème: établir les liens entre chacun des nœuds d'un groupe à chaque nœud de l'autre. C'est un graphe coplanaire. La généralisation consiste à établir les liens entre k nœuds dans un groupe et h nœuds dans l'autre. La théorie s'appuie sur un théorème pratiquement évident, poussé dans ses retranchements: Il n'est pas possible d'aller d'un pays à un autre sans traverser la frontière. Ce graphe est connu comme étant le K3,3. un graphe planaire complet biparti.

Voir	Voir haut de page Croisements dans les graphes Énigme des cinq princes Graphe – Index Les 21 problèmes de Karp – Logique Vocabulaire des graphes
Aussi	Carré latin – Construction Énigmes – Index Numéros des villas Partage – Énigmes classiques Quel est le numéro de la villa?
Sites	Les trois maisons – Wikipédia – Avec développements topologiques Utility Graph – Wolfram MathWorld
Cette page	http://villemin.gerard.free.fr/aJeux1/Topologi/Maison.htm