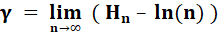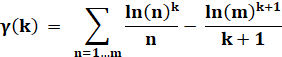|
|||||||||||||||||||||||||||||||||||
![]()
|
CONSTANTE D'EULER-MASCHERONI Constante, calculée par
Leonhard Euler avec 15 décimales et
qu'il a nommée gamma en 1781 puis utilisée par Lorenzo Mascheroni en 1790
avec 19 décimales. En 2009, de l'ordre de 30 milliards de décimales sont
connues.
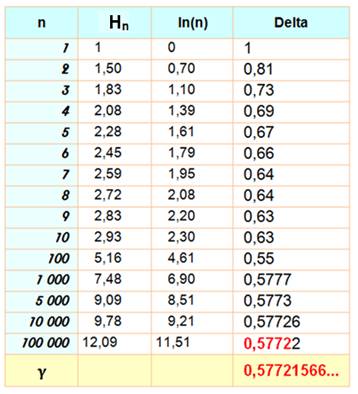
Limite de la différence
entre la série harmonique et le logarithme naturel. Son nom ne provient ni
d'Euler ni de Mascheroni mais fut donné plus tard (1835) du fait de sa
relation avec la fonction
gamma. Depuis août 2017, cette
constante est connue avec 477 milliards de décimales (Ron Watkins) L'exponentielle unité (e) est
parfois appelée la constante d'Euler ou nombre d'Euler. |
|
|
|
|
Idée
Cette
suite est connue sous le nom de série
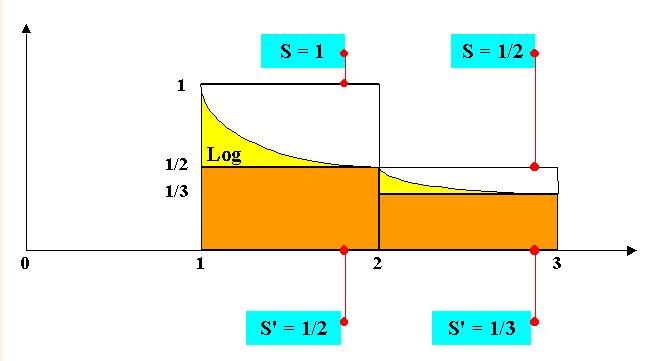
harmonique: On
calcule la somme
On
arrive vite sur la fonction logarithmique:
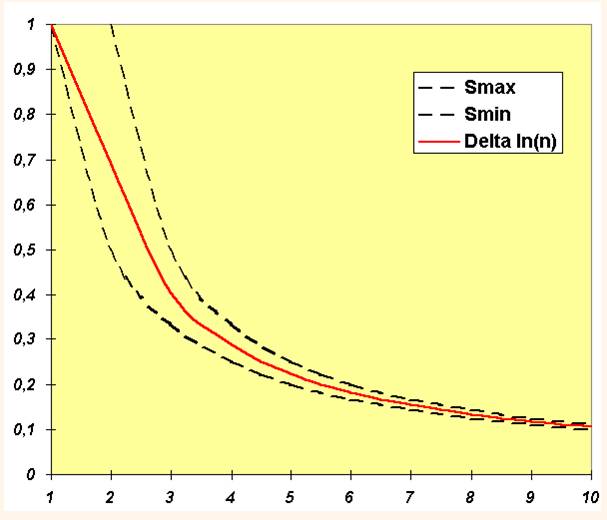
ln (n) Allure des deux fonctions
|
|
|
Hn – ln(n) = Constante pour n infini.
|
|
|
||
|
100
décimales |
5772156649
0153286060 6512090082 4024310421 5933593992 3598805767
2348848677 2677766467 0936947063 2917467495 ... Record: 7 286 255
décimales en 1998 par Xavier Gourdon avec 47 heures de calcul. Voir Mnémotechnique |
|
|
Expressions
|
Limite
formulée simplement
Avec Hn
= 1 + 1/2 + 1/3 + 1/4... série
harmonique. |
|
|
Limite
en somme abrégée
|
||
|
Série
|
||
|
Nature |
On ignore toujours si
cette constante d'Euler (1781) est Si, un jour, on
trouvera une fraction
rationnelle (gamma = a/b), |
|
|
Puissances |
|
|
|
Approximations |
|
|
|
Cas en racine de 3 – Curiosité |
|
|
|
Relation |
Soit un écart avec gamma de 0,000648… Formule due à Eric Weisstein |
|
|
Calcul |
À chaque calcul,
avec la formule donnant gamma, le nombre de décimales
supplémentaires est faible. En effet la série harmonique diverge, mais très,
très lentement. Young a montré que
la convergence est linéaire en n. Euler a utilisé une
autre formule un peu plus rapide (Sommation d'Euler-Maclaurin). On connaît des
formule donnant Pour gamma
, on ne connaît même pas un algorithme qui doublerait le nombre de décimales.
|
|
Propriétés |
On connaît de nombreuses
de nombreuses séries infinies donnant gamma. De même que des
intégrales définies. Gamma intervient aussi
en probabilité: Quelle est la probabilité que deux facteurs irréductibles
d'un polynôme F(x) ne soient pas de même degré pour p
aussi grand que l'on veut ? C'est Voir Toutes
ces formules impliquant la constante d'Euler par Xavier Gourdon. |
Voir Algorithme
|
|
|
|
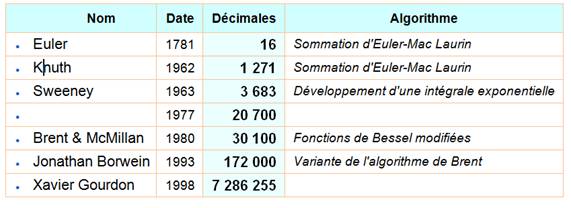
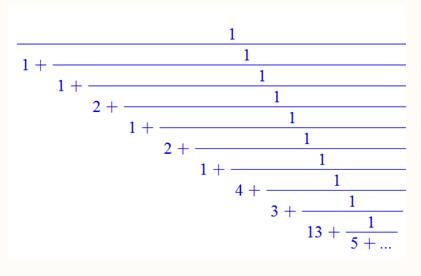
[0, 1,
1, 2, 1, 2, 1, 4, 3, 13, 5, 1, 1, 8, 1, 2, 4, 1, 1, 40, 1, 11, 3,
7, 1, 7, 1, 1, 5, 1, 49, 4, 1, 65, 1, 4, 7, 11, 1, 399, 2, 1, 3, 2, 1, 2, 1,
5, 3, 2, 1, 10, 1, 1, 1, 1, 2, 1, 1, 3, 1, 4, 1, 1, 2, 5, 1, 3, 6, 2, 1, 2,
1, 1, 1, 2, 1, 3, 16, 8, 1, 1, 2, 16, 6, 1, 2, 2, 1, 7, 2, 1, 1, 1, 3, 1, 2,
1, 2, 13, 5, ...]
|
|
|
|
|
|
Smax = Sh Smin = Sh – 1 ln (n) – ln (n – 1)
En
fait,
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Dirichlet
Nd = ln n + 2 Voir formule
donnant la quantité de diviseurs d'un nombre.
Premier
Exemple 43
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
Avec dzêta de Riemann
Voir Riemann Avec les nombres premiers: Formule de
Mertens
Autre formule Avec la dérivée de
la fonction factorielle généralisée
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Gamma ( k )
Valeurs
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
![]()
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Sites |
|
|
Cette page |
![]()