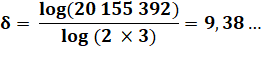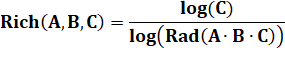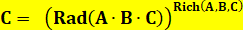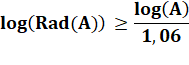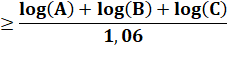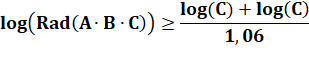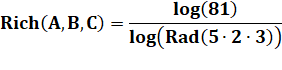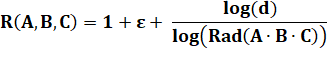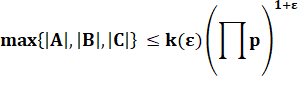|
|||||||||||||||||||||||||||||
![]()
|
CONJECTURE ABC Conjecture d'Oesterlé-Masser Problème d'analyse diophantienne. Appréciation de la quantité de
facteurs répétitifs dans deux nombres et leur somme. La conjecture dit en gros
que: si les facteurs de A et de B sont très répétitifs, alors il y a de
peu de chances pour que les facteurs de la somme C le soient aussi. ou encore: si deux nombres sont riches,
leur somme l'est rarement. Importance de la conjecture.
Si elle était prouvée alors seraient également prouvés
|
|
|
||
|
Exemple 1
|
A= 1 024 B = 81 C = 1 024 + 81 = 1 105 1024 + 81 = 1105 210 + 34 = 5 x 13 x 17 2 x 3 x 5 x 13 x 17 = 13 260 13 260 > 1 105 Deux nombres a et b sans facteurs communs et leur somme c: Le produit des facteurs r(abc) est plus grand que la somme (c). Autrement dit, le nombre abc n'est pas très composé. Ou encore, le
ratio r(abc) / c est très petit. |
|
|
Exemple 2
|
3 + 125 = 128 3 + 53 = 27 3 x 5 x 2 = 30 30 < 128 |
|
|
Ce qui est constaté par l'expérience
|
En général: r(A.B.C) > C Exceptions: r(A.B.C) < C r(A.B.C) K K = 1 engendre une infinité
d'exceptions. K = 1 +
La conjecture ABC formalise ces constats, sous une forme un peu plus
compliquée. |
|
Inspiré de la vidéo
en anglais sur
Numberphile
|
|
||
|
|
108 + 108 = 216 22 x 33 +
22 x 33 = 23
x 33 108 x 108 x 216 = 2 519 424 = 27 x 39
|
|
|
En augmentant A et B, tout en conservant
un petit radical, la richesse du produit ABC est aussi grande que l'on veut. |
216 + 216 = 432 23 x 33 +
23 x 33 = 24
x 33 216 x 216 x 432 = 20 155 392 = 210 x 39
|
|
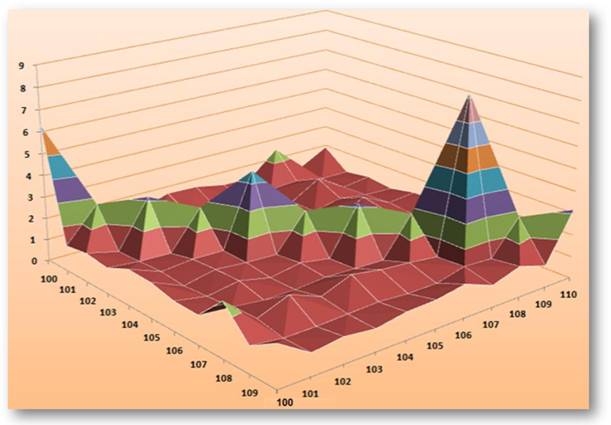
Exemple de calcul de
richesse des triplets de 100 à 110.
La nappe représente la richesse du
triplet (A, B, A+B)
|
|
||
|
|
|
|
|
|
Richesse moyenne |
|
|
|
A et B premiers
entre eux C = A
+ B |
|
|
|
|
|
|
|
|
|
|
|
Plus A et B sont grands, plus l'inégalité est
grande.
|
|
|
|
|
|
Lorsque les trois nombres sont grands et
pas riches, plus la somme C est inférieure à la racine du radical du produit
des trois nombres. |
|
|
||
|
|
Rich moyen = 0,38 … < 0,53, la valeur
calculée Mais nous sommes dans la moyenne des
"pauvres". Avec les très riches quelle est la borne si elle existe? |
|
|
|
Rich moyen = 0, 70 … Rich maximale < 2. Elle atteint rarement des valeurs un peu supérieures
à 1. Il existe sans doute une borne supérieure
(conjecture) |
|
|
|
|
|
|
|
|||
|
|
Avec d'une constante à choisir. On cherche à borner epsilon. |
||
|
|
Pour
une valeur appropriée de d, sans doute très grande, il suffit de prendre
epsilon supérieur à 0, mais aussi proche de 0 que l'on veut. |
||
|
|
Pour
tout nombre réel
Avec log(d) qui dépend d'epsilon. |
||
|
|
Pour
tout nombre réel
Produit pour tout p premier divisant le produit abc Autrement dit: le produit
parcourt tous les facteurs premiers p de abc, soit tous les facteurs présent
dans le radical du nombre. La max indiqué, dans la
mesure où C est la somme de A et B, est égal à C. La constante k grandit indéfiniment au fur et à mesure que epsilon
diminue. |
||
|
|
||
|
|
{2, 310 x 109, 235} Dont la richesse est: 5 log(23) / log(15 042) = 1,629 911 684… Dans la plage indiquée, il y a environ 200
triplets dont la richesse excède 1,4. |
|
|
English
corner |
|
|
|
|
The Boston Globe - November 04, 2012
![]()
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Documents |
|
|
Cette page |
http://villemin.gerard.free.fr/aMaths/Factorisation/ConjABC.htm |
![]()