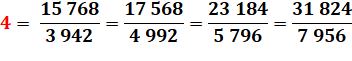|
Édition du: 01/03/2025 |
|
Dictionnaire des Nombres |
||||||||||||
|
100 / 200 |
||||||||||||
|
Nombre 4 |
Culture 4 |
Maths 4 |
Expressions
en 4 |
|
|
Débutant
4 |
Culture
4 (suite) |
Proverbes
avec 4 |
||
|
Sciences 4 |
Sciences
4 (suite) |
|||
![]()
|
|
Nouvelle
orthographe avec
des traits d'union partout |
|||
|
Voir Partitions |
||||
|
Caractérisation du nombre
|
|
Voir |
||
Rappel
Propriétés générales >>>
![]()
|
Comment passer de quatre à un! Papa, explique-moi, c'est quoi être
saoul? - Tu vois les deux barmen. Si
j'étais saoul, j'en verrais quatre. - Mais papa, il n'y en a qu'un! Voir Pensées & humour |
Soit 20 nombres
entiers inférieurs à 70. Leurs
différences deux à deux. Parmi
elles, il y a quatre nombres égaux. Preuve ? |
Quatre chez les Romains dans Astérix

Voir Nombres
romains
Source image:
nombreux sites que vous pouvez retrouver avec Google image ![]()
![]()
PROPRIÉTÉS MATHÉMATIQUES
générales
|
Certaines peuplades
(Papouasie, langue Yupno,) comptaient: 1, 2, 3, 2+2,
5 … |
>>> |
|
|
Premier nombre composé. |
||
|
Premier vrai nombre
carré. Premier
carré d'un nombre premier.
Alors,
le nombre 4 est le seul carré d'un nombre premier qui suit et qui précède un
nombre premier. Merci Fabien T. |
||
|
Motif
exceptionnel avec 2. Nombre
rigolo:
somme
de ses chiffres égal somme des chiffres de ses facteurs. Seul
cas avec (4 + 8 = 12 et 4 x 8 = 32) où les unités de la somme et du produit sont
égales (hors cas trivial du zéro). |
|
|
|
Seul
cas avec (…4 + …8 = …2 et …4 x …8 = …2) où les unités de la somme et du produit sont
égales (hors cas trivial du zéro). |
||
|
Il n'y a que trois cas
comme celui-ci. |
||
|
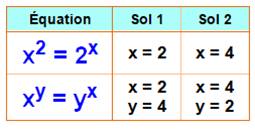
Seule
solutions de ce type. |
||
|
au lieu du IV en chiffres romains classiques. |
||
|
4
x 4 x 4 – 4 = 44 + 4 x 4 = 60 … Célèbre
défi des nombres formés avec quatre 4. |
||
|
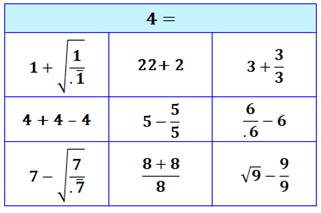
Faire 4 avec k chiffres identiques. |
||
|
|
||
|
= 16 h = 4 x 4
heures Curiosité
de Jérémy (un Internaute) |
||
|
Triplet de Pythagore,
le plus petit. |
||
|
n = 4 est au centre de
nombres (3 et 5) |
||
|
|
||
|
Théorème de Lagrange
(1770): tout nombre est somme de quatre carrés au plus. |
||
|
concernant les nombres premiers. |
||
|
Toutes les
équations de degré 4 ou inférieur sont résolubles par radicaux (utilisation de
racines). Pas généralement possibles pour le 5e degré. |
||
|
|
||
|
Polygone constructible
à la règle et au compas |
||
|
|
||
|
dans le triangle de Pythagore (9, 40, 41) |
||
|
|
||
|
|
||
|
|
||
|
|
![]()
PROPRIÉTÉS MATHÉMATIQUES
détaillées
Chiffres et numération
|
4 |
|
Type
séquence
|
1,
1, 2, 4, 7, 13, 24, 44, 81, 149 … |
|
|
4,
14, 194 … |
|
|
4 = 1 + 1 + 1 + 1 = 2 + 1 + 1 = 2 + 2 = 3 + 1 = 4 |
|
|
4 =
1 + 3 |
|
|
4 =
1 + 3 = 3 + 1 = 1 + 0 + 3 et 13, 31,
103 sont premiers |
Exemple
de la conjecture: il est toujours possible d'obtenir k, non-multiple de
3, avec la somme des chiffres d'un nombre premier. |
|
4
+ 5 + 6 = 7 + 8 |
|
|
4 =
(1+1) + (1-1) + (1x1) + (1/1) |
|
|
4 = 1 + 3 =
2 + 2 8 = 3 + 5 = 4 + 4 12
= 5 + 7 = 6 + 6 |
ou par l'addition d'un
pair à lui-même. |
|
4
= 4 |
|
|
4 |
|
|
|
|
|
|
Voir problème des quatre 4. |
![]()
Table
de multiplication du 4

Voir Table
complète
Multiplication
|
4 =
½ ( 3 x 1² + 3 x 1 + 2 ) |
|
|
4 =
2 x 3 x 4 / 6 |
|
|
4 =
1 + 3 = (2 x 3 x 4) / 6 |
|
|
4!
+ 1 = 5² = 25 5!
+ 1 = 11² = 121 7! + 1 = 71² = 5 041 |
|
Division et diviseurs
|
{1,
2, 4} | 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Phi
est la quantité de nombres premiers inférieurs ou égaux à n. |
|
|
3, [4,
49] 4 = 2² et 5 = 5 => 5 – 2 = 3 |
Seul
49 partage cette propriété (n au moins jusqu'à 109). |
|
|
est divisible
par 4 si 2d+u est divisible par 4. |
4 936
=> 2x3 + 6
= 12 => divisible par 4. |
|
n²
– 1 = (n – 1) (n + 1) est divisible
par 4 si n est impair. |
(3 – 1) (3 + 1) = 8 (5 – 1) (5 + 1) = 24 |
|
x2
– y2 est divisible par 4 si (x – y) est pair. |
32 – 12 = 8 42 – 22 = 12 52 – 32 = 16 |
|
a
= ...cdu
est divisible par 4 si 2d + u
multiple de 4 |
|
|
4
ne
divise pas (4
– 1) ! = 3 ! |
Voir factorielle |
|
a²
+ b² = 4k + r r
= {0,1,2} jamais 3 |
|
![]()
Dénombrement et divers
|
4 =
C41 = C43 |
|
|
4!
– 1 = 23 |
|
|
4 =
00 x 11 x 22 |
|
|
+ 4x(0,5)3
+ … |
|
Puissance

|
4 =
2² = 1 + 3 |
|
|
4 =
2² = 1² + 3 x 1² |
|
|
4 =
23 – 22 = 62 – 25 = 53
– 112 |
|
|
|
|
|
N
= a² + b² si … |
|
|
–4 = (1 + i)4 = (1 – i)4 = (1 + i)3 + (1 – I)3 |
|
|
–1024 = (4 + 4i)4 = (4 – 4i)4 |
|
|
n4 = 16k ou 16k + 1 |
|
Nombres doublement pairs (divisibles par 4)
|
Théorème Tous les
multiples de 4 (sauf 4) sont, au moins une fois, différence de deux carrés.
Les autres nombres pairs ne sont jamais différence de deux carrés. Il suffit
de considérer un des produits de deux nombres pairs (a٠b) et d'appliquer une identité remarquable: Exemple
Record
de présentations |
![]()
Nombre
et ses puissances
|
11
+ 22 + 33 + 44 =
1! × 2! × 3! × 4! 1 + 4 + 27 + 256 = 1 × 2 × 6 × 24 =
288 |
|
|
|
4²
= 5² – 3² |
|
|
|
4, 16,
37, 58, 89, 145, 42, 20, 4 |
|
|
|
2
et 4
|
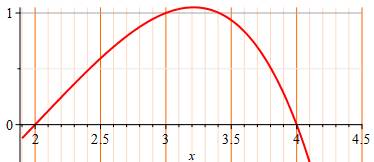
Graphe de la fonction x^2 – 2^x
|
|
|
42 – 1 =
15 44 – 1 =
255 46 – 1 =
4095 48 – 1 = 65535 … 4n |
Sinon (impair): divisible par 3. |
|
|
43 = 82 = 64 |
|
|
|
44 = 256
et 54 = 625 |
|
|
|
44 = 43 + 43 + 43
+ 43 = 256 |
|
|
|
46 = 4 096 |
|
|
|
4n + n4 |
|
|
|
910 = 3 486 784 401 |
|
|
|
|
|
|
|
Voir Explication des notations en
nombre 1/3 Voir Nombre 24 |
|
|
|
|
4 x
1 782 = 71 28 4 x
2 178 = 87 12 4 x 16 782 = 671 28 4 x 16 799 = 671 96 4 x 16 979 = 679 16 … |
|
Autour de ce nombre
|
1/4
= 0,25 2/4
= 0,5 3/4
= 0,75 4/4
= 1 |
soit les deux décimales
25, soit la décimale 5, soit les deux décimales 75, soit entiers (divisible par 4). |
|
|
– 4
= (1 – i )4 = (1 – i)² (1
– i)² = (2i)² 4 = |1 – i |4 =
{ |
|
|
|
95 8004 + 217 5194 + 414 5604
= 422 4814 = 31 858
749 840 007 945 920 321 = 2, 18… 1022 |
|
|
![]()
|
|
||
|
Énigme Soit 20 nombres entiers inférieurs à 70. Leurs différences deux à deux. Parmi elles, il y a quatre nombres égaux. |
Anglais Twenty pairwise
distinct positive integers are all less than 70. Prove that among their
pairwise differences there are four equal numbers. Problème
posé lors d'une compétition junior au Georgia Institute of Technology
en 2009 |
|
|
Solution Prenons les
différences entre deux nombres voisins après avoir ordonné la liste du plus
petit au plus grand. Supposons qu'il n'y
ait pas plus de trois différences égales. Calculons la somme minimale de ces différences => |
Évaluation des différences au mieux Avec 20 nombres, il y
a 19 différences. Et, 19 = 3 x 6 + 1. Dans le cas le plus
optimiste, il y a trois différences égales à 1, puis trois égales à 2, etc. et
la dernière égale à 7. Au total: 3 x
(1+2+3+4+5+6) + 1x7 = 3 x 21 + 7 = 70. |
|
|
Exemples Une combinaison possible de 20 nombres jusqu'à 71 avec
pas plus de trois sommes égales => C'est l'amplitude minimale avec 20 nombres. |
Nombres Différences |
|
|
Principe des tiroirs Si on demande à
réduire cette amplitude de 71 à 69, il faut loger une nouvelle différence égale
à une des différences déjà existantes. D'où présence d'une
quatrième somme. |
Nombres Différences |
|
|
Autre vision,
avec la somme générale des différences.
Elle ne dépasse pas 68. => Or, pour disposer de
trois sommes seulement, la somme minimale
doit atteindre 71. C'est incompatible. Il
faut donc plus de trois sommes égales. |
(a20 – a19) + (a19 – a18) + … Maximum: 69 – 1 = 68 |
|
Retour / Principe
des tiroirs / Jeux et énigmes – Index
|
|
Voir Diviseurs, Quantité,
Somme,
Fonctions
arithmétiques
|
Numération: base, [chiffres] |
Repdigit (Brésilien) |
|
2,
[1, 0, 0] 3, [1, 1] 4,
[1, 0] |
3,
[1, 1] |
Voir Bases
/ Brésiliens
![]()
|
Suite |
|
|
Voir |
|
|
Site |
|
|
Cette page |
![]()
Renvoi de liens
Somme de n carrés >>>
Par couples >>>