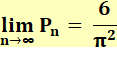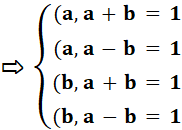NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 28/01/2019 Orientation générale  DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique Brèves de Maths
	Théorie des Nombres
Débutants Général	DIVISIBILITÉ				Glossaire Général
INDEX Calcul Théorie des nombres		PGCD	Algorithme d'Euclide	Premiers entre eux
		PPCM		Pgcd / Ppcm / Racine
		Sommaire de cette page >>> Approche >>> Premiers entre eux >>> Propriétés – Particulières >>> Propriétés – Générales >>> Premiers par paires >>> Théorème de Cesaro >>> Propriétés avec somme, différence et produit >>> Somme et différence: a + b et a – b >>> Somme et produit: a + b et ab >>> Avec des carrés

NOMBRES PREMIERS ENTRE EUX

ou ÉTRANGERS

On connaît les nombres premiers.

On peut étendre cette notion à des groupes de nombres.

Lorsqu'on cherche à rendre une fraction irréductible, les nombres au numérateur et au dénominateur sont premiers entre eux.

30	=	2 x 3 x 5	=	3	3 et 7 sont étrangers ou premiers entre eux (PEE)
70		2 x 5 x 7		7

Deux nombres premiers sont toujours étrangers. Exemple: 11 et 13 Mais, ceci n'est pas nécessaire. Exemple: 8 et 9 sont étrangers sans être premiers ni l'un ni l'autre.

Deux nombres étrangers n'ont pas de diviseurs communs. Leur plus grand commun diviseur (PGCD) est 1. Notation abrégée: (a , b) = 1

Anglais: a and b are relatively prime or coprimes.

Approche

A, B, C …. sont premiers entre eux s'ils n'ont que 1 comme diviseur commun.

PGCD (A, B, C …) = 1

A = 11	= 1 x 11
B = 21	= 1 x 3 x 7
PGCD (A, B)	= 1

On dit que:

11 et 21 sont premiers entre eux

ou étrangers

A = 11	= 1 x 11
B = 21	= 1 x 3 x 7
C = 25	= 1 x 5 x 5
PGCD (A, B, C)	= 1

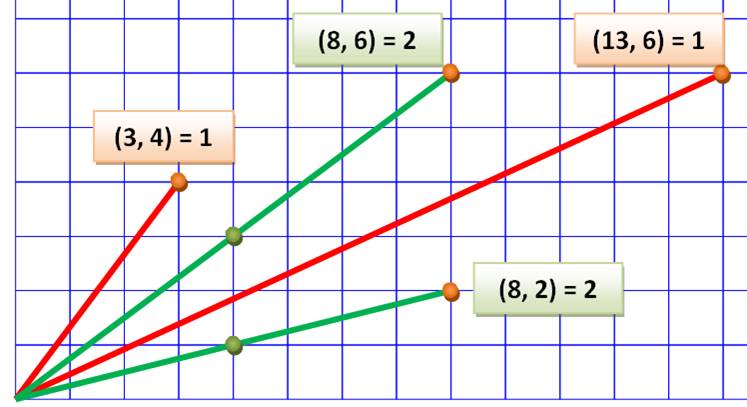
Approche illustrée

Deux nombres sont premiers entre eux si le segment qui les représente (en rouge) ne passe par aucun point de la grille. Dans le cas contraire (en vert), le premier point d'intersection (vert) représente deux nombres effectivement premiers entre eux.

Table des PGCD & nombres étrangers

Établissons la table des PGCD

& Observons

La symétrie du tableau

Car PGCD (A, B) = PGCD (B, A).

Les enfilades de 1 lorsque le nombre est premier jusqu'à rencontrer son multiple.

Voir 7 en particulier.

Les cycles sur les lignes n : le motif se répète avec une période égale à n.

En ligne 3, on trouve: 1, 1, 3, 1, 1, 3 ….

Mêmes cycles sur les colonnes.
Du fait de la symétrie du tableau.

PGCD des nombres de 1 à 10

	1	2	3	4	5	6	7	8	9	10
1	1	1	1	1	1	1	1	1	1	1
2	1	2	1	2	1	2	1	2	1	2
3	1	1	3	1	1	3	1	1	3	1
4	1	2	1	4	1	2	1	4	1	2
5	1	1	1	1	5	1	1	1	1	5
6	1	2	3	2	1	6	1	2	3	2
7	1	1	1	1	1	1	7	1	1	1
8	1	2	1	4	1	2	1	8	1	2
9	1	1	3	1	1	3	1	1	9	1
10	1	2	1	2	5	2	1	2	1	10

On laisse en blanc les cases

des nombres premiers entre eux.

Grilles des premiers en eux (PEE en noir)

Ces grilles sont symétriques par rapport à la diagonale descendante.

Zones de carrés blancs: nombres successifs non premiers entre eux

Le cercle rouge indique le premier carré 2x2 avec quatre nombres non-PEE. Coordonnées du coin: (14, 20). Illustration ci-dessous.

Le premier carré 3x3 non-PEE est en (104, 6 200):

Recherche d'un carré 3x3

Prenons n et m impairs. Alors, les quatre coins seront pairs. Sur la colonne centrale, n est impair, prenons 3 et pour les deux autres facteurs 5 et 7 et voyons. n = 3 x 5 + 7 = 105.

Alors n -1 = 104 = 2³ x 13 et 106 = 2 x 53. Ce qui induit que m = k x 3 x 13 x 53 = 2 067. Un essai montre que k = 1 ou 2 ne conviennent pas et que k = 3 donne une solution.

On imagine que cet exemple est le plus petit. Une exploration par programme le confirme.

Programmation Maple du dessin des grilles montrées ci-dessus

Statistics:−HeatMap(Matrix(15,(i,j)→`if`(AreCoprime(i,j),1,0)),color=["White","Red"]);

Table des nombres premiers entre eux jusqu'à 50

Lecture: n = 10; il y a quatre premiers avec 10; ce sont: 1, 3, 7, 9 dont 3 et 7 sont premiers (rouge)

Voir Tables

Une liste très limitée

Nombres dont tous les premiers avec eux sont également premiers

(ligne jaune avec tous les nombres en rouge):

2, 3, 8, 12, 18, 24, 30.

Et c'est tout!

Propriétés particulières

Propriété

n et

n + 1 2n + 1 … k.n + 1

Sont premiers entre eux.

Exemple

n	m = k.n + 1	PGCD (n, m)
7	8	1
	15	1
	22	1
	29	1
	36	1
	43	1
	50	1
	57	1
	64	1
	71	1

Fibonacci

F_n et F_n+1 sont premiers entre eux.

Deux termes voisins de la suite de Fibonacci sont premiers entre eux.

Exemple

1	1	2	3	5	8	13	21	34	55	…
		P
		P	P
			P	P
				P	2^3
					2^3	P
						P	3.7
							3.7	2.17
								2.17	5.11

Propriétés générales

Théorème de caractérisation

des nombres premiers entre eux

S'il existe deux nombres x et y

tels que ax + by = 1

alors a et b sont premiers entre eux

a et b > 0.

Démonstration

Directe
Si a et b premiers entre eux	PGCD = 1
Théorème de Bachet - Bézout Il existe x et y tels que	ax + by = 1
Inverse
S'il existe x et y tels que	ax + by = 1
Si d divise a et b , il divise aussi	ax et by
Donc d divise	ax + by
Or	ax + by = 1
Si d divise l'unité, il ne peut être que	1
Et	a et b sont premiers entre eux

Puissances

Voir Autres propriétés

Liste finie

Quels sont les nombres n tels que tous les nombres impairs premiers avec n sont tous des nombres premiers ? Ils sont seize:

[2, 3, 4, 5, 6, 7, 8, 9, 12, 15, 18, 21, 24, 30, 45, 105]

Premiers par paires – Nombres a1 , a2 , … , an
Général	Par paires
Nombres premiers entre eux. Nombres étrangers. Relatively prime. Ils sont tous premiers entre eux. Anglais: Coprime ( a1 , a2 , … , an ) = 1	Nombres premiers entre eux par paires. Nombres étrangers par pairs. Relatively prime in pairs. Ils sont premiers entre eux deux par deux. Pairwise coprimes ( ai , aj ) = 1 pour tous

Théorème de Cesaro
0,607927102 …	Probabilité que deux nombres n'aient aucun diviseur commun. Cad: Probabilité que deux nombres pris au hasard soient premiers entre eux. Probabilité qu'un nombre ne soit pas divisible par un carré. Densité asymptotique des nombres sans carré.
Théorème de Cesàrio (1859-1906), démontré en 1881). Pour tout n, la probabilité Pn que deux nombres entiers choisis au hasard et inférieurs à n soient premiers entre eux est exprimée par la limite suivante: Le calcul de zêta (2) = pi/6, dit problème de Bâle, est dû à Euler en 1735.

Résumé des propriétés

(voir ci-dessous)

que si a et b sont de parité opposée (voir ci-dessous)

Exemples de calculs (PEE = premiers entre eux)
Si a et b sont PEE, alors a et b sont PEE avec la somme d'une part et avec la différence d'autre part. Si on connait un nombre n = p.q, avec p et q premiers entre eux, alors le nombre p + q est premier avec n (p,q) = 1 (p.q, p+q) = 1 Ex: n = 15 = 3 x 5 et 8 est premier avec 15 comme 2 d'ailleurs Théorème de Dirichlet Pour tout a et b étant PEE positifs, il existe une infinité de nombres premiers du type a + bx, Voir Forme des premiers	On sait que a et b sont PEE: a ne divise pas b et b ne divise pas a. Avec a + b, a divise le premier terme mais pas le second; b divise le second pas le premier. a + b est premier avec a et avec b. Même chose avec a – b Démonstration alternative Relation de Bézout: au + bv = 1 au + bv + av – av = 1 au – av + av + bv = 1 a(u – v) + (a + b)v = 1 aU + (a + b)V = 1 Les nombre a et a + b sont PEE.

Si a et b sont PEE et de parité opposée, alors leur somme et différence sont PEE. Exemples a et b étant PPE Lorsque la parité est opposée, la somme et la différence sont PPE.

Examinons la parité Si a et b sont pairs, somme et différence sont paires et ne sont donc pas PEE (Voir le rappel en pied de chapitre). Si a et b sont impairs, somme et différence sont paires et ne sont donc pas PEE. Pour que somme et différence soient PEE, il est nécessaire que a et b soient de parité opposée. Mais ce n'est pas suffisant comme le montre cet exemple: 6 + 3 = 9 et 6 – 3 = 3. On constate que dans ce cas les nombres a = 6 et b = 3 sont bien de parité opposée, mais (a et b) comme (a+b et a–b) ne sont pas PEE. Nécessité d'être premiers entre eux Donc a et b doivent être de parité opposée; mais, que faut-il en plus? Prenons le cas où a et b partagent un facteur commun g. a = ga' et b = gb' Alors: a + b = g (a' + b') a – b = g (a' – b') Somme et produit partagent aussi ce même facteur commun, et ils ne sont donc pas PEE. Pour être PEE, il faut que g = 1. Ce qui veut dire que les nombres a et b doivent être aussi PEE. Rappel Supposons a et b de même parité. Si pairs (P): a + b P + P P a – b P – P P Si impairs (I): a + b I + I P a – b I – I P Si a et b sont de même parité alors a + b comme a – b sont divisibles par 2.

Somme et produit
Théorème Si a et b sont PEE, alors a.b et a+b sont PEE. Rappel du lemme d'Euclide Si p, un nombre premier divise a.b, deux nombres entiers relatifs, alors p divise a ou b.		Démonstration 1 Supposons que p, un nombre premier, divise a.b et a + b Si p divise a.b, il divise a ou b; disons a (sinon, on inverse). Or p divise (a + b), il divise déjà a, il doit aussi diviser b. On peut le monter en faisant p diviser la somme algébrique: (a+b) – a = b. Divisant à la fois a et b, p serait un facteur commun. Ce qui contraire à notre hypothèse. Alors p = 1 et a.b est a + b sont PEE.
Rappel sur la relation de Bézout Les nombres a et b sont PEE, si et seulement s'il existe deux nombres entiers relatifs (u et v) tels que: au + bv = 1		Démonstration 2 au + bv = 1 (au + bv)² = 1 (au)² + 2aubv + (bv)² = 1
Suite	(au)² + 2aubv + (bv)² + abu² – abu² + abv² - abv² = 1 a²u² + abv² + abu² + b²v² – abu² + 2abuv – abv² = 1 (a + b) (au² + bv²) – ab (u – v)² = 1 (a + b) U + ab V = 1 Bézout => a + b et a.b sont PEE

Avec des carrés
Théorème Si a et b sont PEE, alors a+b et a² – ab + b² sont PEE ou divisible par 3	Soit d un diviseur commun à a + b et a² – ab + b², alors: d | a + b  et d | a² – ab + b² d | (a + b)² et d | a² – ab + b² d | (a + b)² – (a² – ab + b²) d | 3ab
Nous avons vu que si a et b sont PEE, alors a + b et ab son PEE: la somme et le produit n'ont aucun facteur en commun. Or d divise la somme, il ne divise pas le produit	(a + b, ab) = 1 d | a + b  => d ∤ ab
Avec le lemme d'Euclide:	d | 3 => d = 1 ou 3
Deux exemples	1 + 5 = 6, 1² – 5 + 25 = 21 et (6, 21) = 3 1 + 6 = 7, 1² – 6 + 36 = 31 et (7, 31) = 1

Suite	Propriétés des nombres premiers entre eux
Voir	Diviseurs: calculs et facteurs premiers Divisibilité dans une suite de nombres Quantité de nombres premiers avec n Totient d'Euler Théorie des nombres – Index Diviseurs: nombres parfaits Nombres Premiers Pseudo Premiers Pseudo Premiers Absolus Fraction continue
DicoNombre	Nombre 0,607 …
Cette page	http://villemin.gerard.free.fr/ThNbDemo/PremEEux.htm