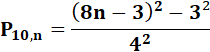type de nombres: nombres décagonaux

Édition du: 25/06/2020

M'écrire

Brèves de Maths

INDEX

Types de nombres figurés: liste et liens

Nombres

Nombres Polygonaux

Ennéagonaux

Décagonaux

Dodécagonaux

Autres

Décagonaux centrés

NOMBRES DÉCAGONAUX

10-gonal

Nombres construits en déposant des points sur des décagones gigognes, chacun appuyé sur le précédent.

Sommaire de cette page

>>> Nombres décagonaux

>>> Nombres décagonaux – Tables

>>> Propriétés avec les nombres entiers

>>> Propriétés avec les nombres triangulaires

>>> Nombres décagonaux généralisés

>>> Langues

Débutants

Nombres figurés ou géométriques

Glossaire

Nombres géométriques

Nombres décagonaux

haut

Construction des nombres décagonaux

n	En plus	E
1	1	1
2	9	10
3	17	27
4	25	52
5	33	85
6	41	126
7	49	175
8	57	232

Observez que le supplément (gnomon) est en 8n + 1.

Notation et formules

La formule en somme résulte du décompte vu ci-dessus. L'incrément étant égal à: 8n + 1

Caractérisation

Sorte de racine décagonale.

Si n est un nombre entier alors x est le énième nombre décagonal. Sinon, il n'est pas hexagonal.

N est une des racines de x = 4n² – 3n

Fonction génératrice

L'instruction demande le développement sur dix termes.

Programme

Somme des inverses des décagonaux

Constante calculée pour n jusqu'à 10 000:
1,21672…

Nombres décagonaux – Tables		haut
Les 100 premiers décagonaux	1, 10, 27, 52, 85, 126, 175, 232, 297, 370, 451, 540, 637, 742, 855, 976, 1105, 1242, 1387, 1540, 1701, 1870, 2047, 2232, 2425, 2626, 2835, 3052, 3277, 3510, 3751, 4000, 4257, 4522, 4795, 5076, 5365, 5662, 5967, 6280, 6601, 6930, 7267, 7612, 7965, 8326, 8695, 9072, 9457, 9850, 10251, 10660, 11077, 11502, 11935, 12376, 12825, 13282, 13747, 14220, 14701, 15190, 15687, 16192, 16705, 17226, 17755, 18292, 18837, 19390, 19951, 20520, 21097, 21682, 22275, 22876, 23485, 24102, 24727, 25360, 26001, 26650, 27307, 27972, 28645, 29326, 30015, 30712, 31417, 32130, 32851, 33580, 34317, 35062, 35815, 36576, 37345, 38122, 38907, 39700
Décagonaux carrés	Aucun (sauf trivial 1).
Décagonaux cubes	27 est le seul jusqu'à 10 millions au moins.

Propriétés avec les nombres entiers		haut
Parité	Cycle: impair-pair.
Unités (hors le premier 1)	0, 7, 2, 5, 6, 5, 2, 7, 0, 1
Somme d'un carré et d'un nombre pronique
Différence de carrés	En effet (8n – 3)² – 3² = 64n² – 48n +9 – 9 = 16(4n² – 3n)

Propriétés avec les nombres triangulaires

haut

P_10,n = T_n + 7T_n-1 (Illustration)

= 1/2 n (n + 1) + 7/2 n (n – 1)

= 1/2 (n² + n + 7n² – 7n)

= 4n² – 3n

2P_10,n = T_4n-2 – 1

= 1/2 (4n – 2)(4n – 1) – 1
= 1/2 (16n² – 12n + 2) – 1
= 8n² – 6n

= 2(4n² – 3n)

Nombres décagonaux généralisés		haut
Décagonaux du deuxième ordre	Même formule que pour les ordinaires avec signe plus.
Les premiers décagonaux du 2^e ordre	7, 22, 45, 76, 115, 162, 217, 280, 351, 430, 517, 612, 715, 826, 945, 1072, 1207, 1350, 1501, 1660, 1827, 2002, 2185, 2376, 2575
Décagonaux généralisés	Soit la réunion des nombres décagonaux ordinaires avec les centrés.
Les premiers décagonaux généralisés (ordinaires et du 2^e ordre)	1, 7, 10, 22, 27, 45, 52, 76, 85, 115, 126, 162, 175, 217, 232, 280, 297, 351, 370, 430, 451, 517, 540, 612, 637, 715, 742, 826, 855, 945, 976, 1072, 1105, 1207, 1242, 1350, 1387, 1501, 1540, 1660, 1701, 1827, 1870, 2002, 2047, 2185, 2232, 2376, 2425, 2575, …

Langues

Anglais: A decagonal number is a figurate number.

Allemand: Decagonalzahl oder Zehneckzahl

Espagnol: Un número decagonal es un número figurado.

Italien: Un numero decagonale è un numero poligonale

Haut de page

Retour	Nombres ennéagonaux
Suite	Nombres décagonaux centrés Nombres hexagonaux Nombre pentagonaux Nombres heptagonaux Nombres octogonaux Nombres dodécagonaux
Voir	Types de nombres figurés – Index
DicoNombre	1 10 27 52 85 >>>
Sites	Décagonal - Dictionnaire de mathématiques récréatives Nombre décagonal – Wikipédia Decagonal Number – Wolfram MathWorld Decagonal numbers – Numbers Aplenty *OEIS A001107 - 10-gonal (or decagonal) numbers: a(n) = n(4n-3)*
Cette page	http://villemin.gerard.free.fr/aNombre/FIGURE/Decagon