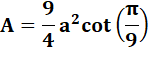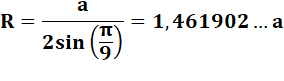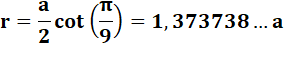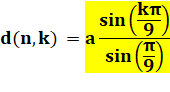|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
Ennéagone – Nonagone
Polygone
à 9 côtés. Il a 9 sommets et 27 diagonales. La somme des angles internes vaut
7 Il
est régulier si les neuf côtés ont même longueur et les angles internes ont
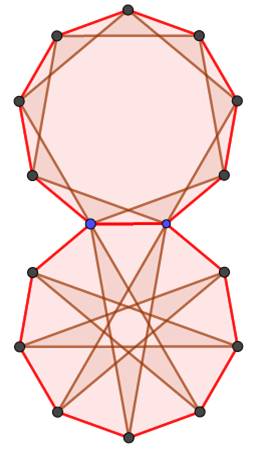
même mesure (140°). Ils sont trois dont deux étoilés. L'ennéagone
régulier est inconstructible à la règle
et au compas. La construction
est faisable avec une règle marquée. Du grec ennéa:
neuf et gônia: angle. Figure plane
à neuf angles et neuf côtés. |
Anglais: nonagon or enneagon
|
|
|||
|
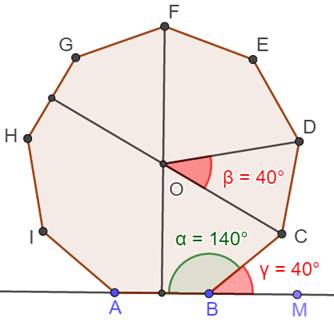
Angles |
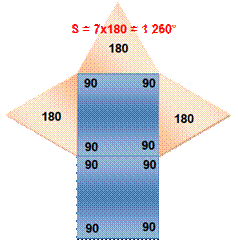
Au centre: 360 / 9 = 40° Au sommet (interne) : (9-2) 180
/ 9 = 140° Au sommet (externe): 180 – 140 = 40°
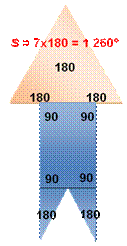
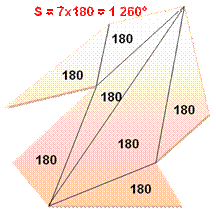
Somme des angles internes: 9 x 140 =
1 260° =
|
||
|
Diagonales |
|
||
|
Aire |
= 6,181824193772900127
… a² |
||
|
Rayon du cercle circonscrit |
|
||
|
Rayon du cercle inscrit ou apothème |
|
||
Voir Construction
de l'heptagone (Neusis)
|
|
|||||||||||||||
|
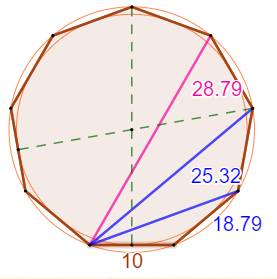
Longueur
de la diagonale k, avec k la quantité de côtés interceptés par la diagonale. |
|
||||||||||||||
|
|
||||||||||||||
Voir Son calcul / Tables / Quantité
d'intersections des diagonales
Cas de l'ennéagone quelconque – Somme des angles internes
|
|
|
|
|
|
|
|
Voir Toutes les autres méthodes de construction (neusis, approximation, calcul d'erreur)
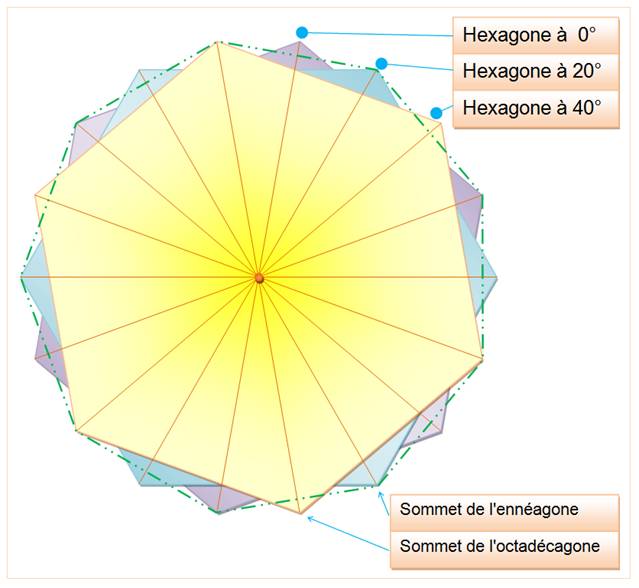
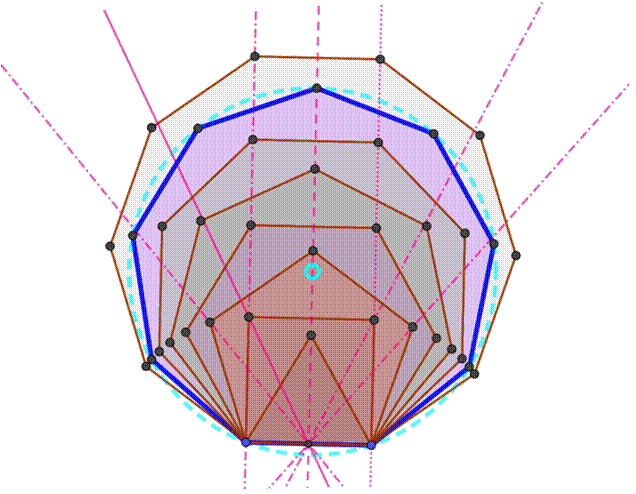
Le cercle divisé par l'ennéagone

|
|
|
|
L'ennéagone (en bleu) avec son cercle circonscrit
et son centre (en bleu clair). Tous les polygones
de 3 à 10 côtés construits sur le même côté. Quelques droites pour vérifier certains alignements ou
pas.
|
|
![]()
|
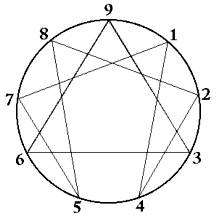
Ennéagramme (nonagramme) mystique datant sans doute de
Babylone, il y a 5 000 ans
|
Nonagramme Athanasius Kircher (1665) Symbole des forces de l'Univers
|
Voir Ésotérisme –Index
![]()
|
Suite |
|
|
Voir |
|
|
Site |
|
|
Cette page |
http://villemin.gerard.free.fr/GeomLAV/Polygone/Enneagon.htm |
![]()