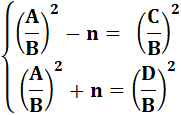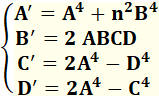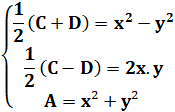|
||||||||||||||||||||||||||||||||||||||||
![]()
|
NOMBRES CONGRUENTS Formules Formules génériques pour créer des nombres congruents. |
|
|
|
|
Suite >>>
Suite >>>
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
2A² = C² + D² = ½ (C-D) + ½ (C+D) 2n.B2 = C2
– D2 = (C – D) (C + D) A4 – n2
.B4 = C2.D2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Les
nombres 1 et 2 ne sont pas congruents
A4 – n2 .B4 = C2.D2
& A4 + n2 .B4 = C2.D2 Avec n = 1
et n = 2: A4 – B4 = C2.D2 &
A4 + B4
= C2.D2 A4 – 4B4 = C2.D2 &
A4 + 4B4 = C2.D2
Avec x et y deux entiers premiers entre eux et de parité
différente.
n. B² = ½ . 4 (x.y) . 2 (x² – y²) = 4
(x.y) (x² – y²)
n. (2b)² = 4 (x.y) (x² – y²) n. b²
= (x.y) (x² – y²)
nprimitif =
(x.y) (x² – y²)
|
|
![]()
|
Suite |
|
|
Voir |
|
|
Diconombre |
|
|
Cette page |
![]()