|
|||||||||||||||||||||||||||||||||||||||||||||
![]()
|
Brique d'Euler et Brique parfaite On
considère le parallélépipède,
ses dimensions et toutes ses diagonales. Il est parfait
si toutes ses mesures sont des nombres entiers
ou alors simplement brique d'Euler si la
grande diagonale manque à l'appel. Il existe
une infinité de briques d'Euler et on ne connait aucune brique parfaite. |
Anglais: Euler Brick / Perfect cuboid
Perfect
parallelepiped / perfect cuboid or perfect box
|
|
|||||
|
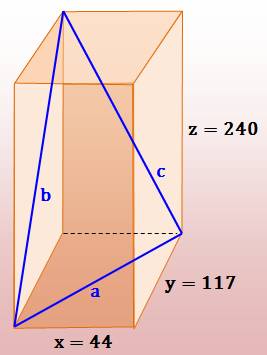
Définition et exemple
x² + y² = a² y² + z² = b² z² + x² = c² Tous
ces nombres étant des nombres entiers.
x = 44, y = 117, z
= 240 |
|
||||
|
Calcul des diagonales
avec le théorème de Pythagore
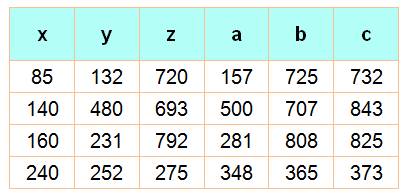
Formule engendrant des
briques d'Euler
Si
(u, v, t) est un triplet de Pythagore: (x,
y, z) = (u (4v² – t²), v (4u² – t²), 4uvt) Alors
les diagonales: (a, b, c) = (t3, u (4v² + t²), v (4u² + t²)) Autres exemples
Conditions
Propriétés
|
|||||
Anglais: parallelepiped
|
|
|||
|
On
va examiner les cas de:
|
|||
|
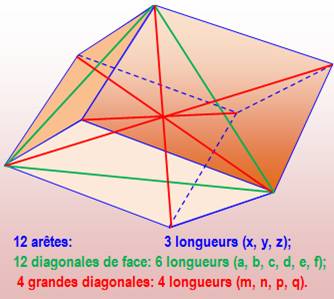
Parallélépipède quelconque les
trois dimensions, les diagonales de face et les grandes diagonales sont des
nombres entiers. Soit 3 + 6 + 4
valeurs en nombres entiers. Note: le pavé étant quelconque (angle pas à
90°), les grandes diagonales sont toutes de longueurs différentes. De même,
pour chacune des deux diagonales d'une face. |
|
||
|
Richard
Guy avait posé la question de l'existence d'un tel pavé. En
2009, Clifford Reiter et Jorge
Sawyer en découvre un grand nombre par exploration systématique sur
ordinateurs, dont celui du tableau. Note: Inutile de vérifier avec le théorème
de Pythagore, les angles ne sont pas de 90°. |
|
||
|
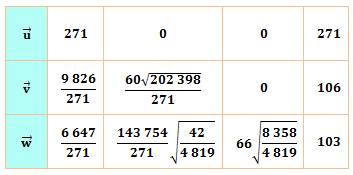
Définition vectorielle
du pavé Les
vecteurs définissant ce
pavé sont les suivants:
|
Calcul des normes
(longueurs) des vecteurs
|
||
|
Parallélépipède droit Avec
deux faces rectangulaires, on connait
quelques pavés parfaits. Par
contre, pour le pavé droit parfait (brique
parfaite), on n'en connait aucun et on ne sait pas s'il peut exister. En tout
cas, la plus petite arête est supérieure à 3000 milliards. Conditions d'existence:
|
|||
|
Parallélépipède droit
presque-parfait |
Arêtes
(672 / 153 / 104) Diagonales
de face (689,19 / 680 / 185) Grande
diagonale (697) Arêtes
(18 720 / Diagonales
de face (23 711 / 16511 / 20 280) Grande
diagonale (24 961) |
||
![]()
|
Retour |
|
|
Voir |
|
|
DicoNombre |
|
|
|
|
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/Addition/ThPythBr.htm |
![]()