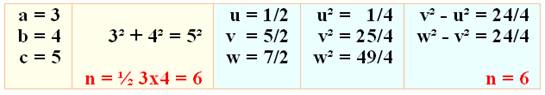NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 29/09/2019 Orientation générale  DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique Brèves de Maths
	Type de nombres
Débutants Nombres	Nombres congruents				Glossaire Nombres
INDEX Nombres	Présentation	Valeurs	Propriétés	Historique
			Formule
		Sommaire de cette page >>> Importance de cette notion >>> Somme et produit >>> Propriétés >>> Carrés en progression arithmétique >>> Courbes elliptiques >>> Recherche >>> Généralisation

NOMBRES CONGRUENTS

Triplets de nombres dont l'écart entre les carrés est identique:

Alors n est dit nombre congruent. C'est aussi un nombre entier donnant l'aire d'un triangle rectangle.

Petit air de famille avec les triplets de Pythagore? En effet!

IMPORTANCE de cette notion

La recherche des nombres congruents est un problème dont l'énoncé est simple, mais dont la résolution mobilise une grande énergie des mathématiciens, d'autant que son énoncé date de l'Antiquité. Les nombres congruents relient plusieurs mondes: les triplets de Pythagore et la géométrie du triangle rectangle; >>> la progression arithmétique entre carrés; >>> la somme de deux carrés valant le double d'un carré; >>> les solutions rationnelles sur les courbes elliptiques. >>>

Somme, produit
Le triplet Somme des termes Produit, en souvenant que le produit de trois carrés est un carré. Le produit des deux extrêmes est aussi un carré.	v² – n , v², v² + n S = 3v² P² = v² (v² – n) (v² + n) = v^6 – n²v² Q² = (v² – n) (v² + n) Exemple avec 1, 25, 49 Produit = 1225 = 35²
Le triplet Somme des termes Différence	u² , v² , w² avec u² + n = v² et v² + n = w² u² + v² + 2n = v² + w² 2n = w² – u² u² – v² = v² – w² 2v² = w² + u²

Propriétés générales

Infinité

Comme pour les triplets de Pythagore, connaître un nombre congruent, c'est en connaître une infinité. Il suffit de le multiplier par un carré. Les côtés sont doublés et l'aire est quadruplée. Ainsi avec le nombre congruent 5, on forme 5 x 4 = 20, 5 x 9 = 45, 5 x 16 = 80 … Les plus petits sont appelés les nombres congruents primitifs.

Il y a donc une infinité de nombres congruents.

Dans ces conditions, les nombres congruents primitifs ne comportent pas de carrés (sans facteur carré ou squarefree). De sorte que le recensement de tels nombres pourra se limiter aux nombres sans facteur carré.

Triplets de Pythagore primitifs

Les triplets primitifs de Pythagore dont le second terme est pair engendrent une série de nombres congruents.

les trois termes sont: (A² – B²), (2AB) et (A² + B²);

Les conditions: A > B > 0; (A,B) = 1; et AB mod 2; et

n = A.B (A² – B²).

Suite en Nombres congruents entiers

Nombre 1

Comme l'a démontré Fermat, le nombre 1 n'est pas congruent. Conséquence: il n'existe aucun carré rationnel qui est congruent.

De même, comme le nombre 1 n'est pas un nombre congruent, le triangle rectangle isocèle (2, 2, 1) n'est pas rationnel, et, par conséquent, racine de deux est irrationnel.

Premiers

En 1952, Heegner démontre: si p 5 mod 8 ou p 7 mod 8 est premier alors p est un nombre congruent.

Si p est un nombre premier, alors:

Congruent	OUI	NON
si p 3 (mod 8)	2p	p
si p 5 (mod 8)	p
si p 7 (mod 8)	p , 2p

Non congruence (résultats de Genocchi - 1855):

Congruent	NON
si p 3 (mod 8)	p
si p 3 (mod 8) et q 3 (mod 8)	p.q
si p –3 (mod 8)	2p
si p –3 (mod 8) et q –3 (mod 8)	2p.q

Heegner et Birch ont trouvé que:

Congruent	OUI
si p –1 (mod 4)	2p

En 1972, Alter, Curtz and Kubota conjecturent que si n = 5, 6 or 7 modulo 8 alors n est un nombre congruent. Démontré en 1975 par Stephens sous réserve de la validité de la conjecture de Birch et Swinnerton-Dyer.

Facteurs

Tout nombre congruent peut s'écrire sous la forme n = k².p.q. (p² – q²).

Voir Valeurs

Carrés en progression arithmétique
Un nombre congruent est l'aire d'un triangle rectangle rationnel; c'est aussi la raison d'une progression arithmétique entre trois carrés. Prenons par exemple 1², 5² et 7². Écart 24 = 2² x 6. Le nombre 24 est congruent, ainsi que 6, lorsqu'on retire le carré. Relations entre les deux notions
	Triangle rectangle rationnel	Progression arithmétique
Formules
Conversion
Exemples

Tables

Triplets de Pythagore et triplets de carrés en progression Remarquez que, pour le "triplet progression", la somme des extrêmes est égale à deux fois le nombre central. u² + w² = 2v². Exemples: 1 + 49 = 50 = 2 x 25 ou 49 + 289 = 338 = 2 x169. Quelques triplets avec le nombre congruent primitif 6

Voir Triplets de Pythagore / Primitifs

Courbes elliptiques
Voici une troisième manière de définir un nombre congruent. Si la courbe elliptique y² = x^3 – n². x contient un point rationnel (y 0), alors n est un nombre congruent. Théorème associé Si trois carrés de nombres rationnels sont en progression arithmétique de raison n, leur produit est un exprimé par la relation: P² = (v² – n) v² (v² + n) = v² (v^4 – n²) = (v²)^3 – v² u² Cette relation établit le fait que, si n est congruent, il existe un point de coordonnées rationnelles sur la courbe elliptique: y² = x^3 – n²x Remarque En 1877, Lucas avait prouvé que n est congruent si et seulement si l'équation suivante a des solutions en nombres positifs rationnels: y² = x^4 – n² Relations avec a, b et c
	Triangle rectangle rationnel	Courbe elliptique
Formules
Conversion
Exemple
Illustration

Voir Nombres congruents: formules et courbes elliptiques / Cercle unité et courbes elliptiques /

Méthode de cryptage / Historique et lemniscate

Fonction elliptique et nombres***

Courbe elliptique E: y² = x³ + ax² + bx + c avec a, b et c .

Avec p premier, N(p) est la quantité de points dans E modulo p.

N(p) est la quantité de solutions (x,y) mod p de l'équation E mod p.

Recherche – Un coup d'œil …

Nature du problème S'il est simple de rechercher des nombres congruents "entiers" avec la formule des triplets de Pythagore, c'est plus difficile avec des nombres fractionnaires. Il faut parfois aller très loin pour un nombre assez petit. Exemples classiques avec les nombres 53, 101 ou 157 Théorème de Tunnell Récemment, ce théorème a permis de progresser dans le recensement des nombres congruents. Voici l'allure de ce théorème: sous réserve de la preuve de la conjecture de Birch et Swinnerton–Dyer. En gros … Cette conjecture ressemble à cela: si E est une courbe elliptique définie sur Q, alors L(E,1) = 0 si et seulement si E a un rang positif. L est une série spécifique associée à la courbe elliptique (Cn). C'est un produit d'inverses de puissances de la forme:

Voir Développements récents

Généralisation – Un coup d'œil …

t-congruent Un nombre est t-congruent, s'il existe des nombres rationnels positifs tels que: Avec le cas classique vu ci-dessus pour t = 1. -congruent Soit un nombre réel compris entre 0 et tel que cos = s/r avec (s,r) = 1, alors n est -congruent si est l'aire d'un traingle ayant des côtés rationnels et un angle . Ces notions sont utilisées pour travailler dans le domaine du recensement des nombres congruents et de la recherche des solutions rationnelles sur les courbes elliptiques.

Voir Triangle héronien et trigonométrie / Cercle unité et triplets de Pythagore

Suite	Nombres congruents – Historique
Voir	Addition - Glossaire Briques de Pythagore Congruence, modulo Pythagore – Biographie Triangle de Pythagore Triangle rectangle
Diconombre	Nombre 5 Nombre 6 Nombre 7 Nombre 13
Sites	Les fonctions elliptiques – Jean-Claude Pénin – 2017
Cette page	http://villemin.gerard.free.fr/aNombre/TYPADD/CongProp.htm