|
|||||||||||||||||||||||||||||
![]()
|
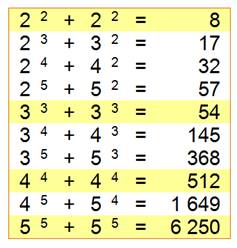
NOMBRES de LEYLAND Nombres à motif en puissance
comme: 100 = 26
+ 62 ou 32 = 24 + 42 qui
est symétrique 32 = 16 + 16. Ces nombres ont été inventés
pour obtenir des nombres le moins typé possible, adéquates pour tester des
algorithmes de recherche de primalité. |
Paul Leyland
|
|
|
|
|
Nombres de la forme
|
|
|
|
|
|
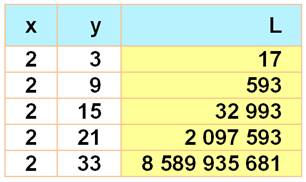
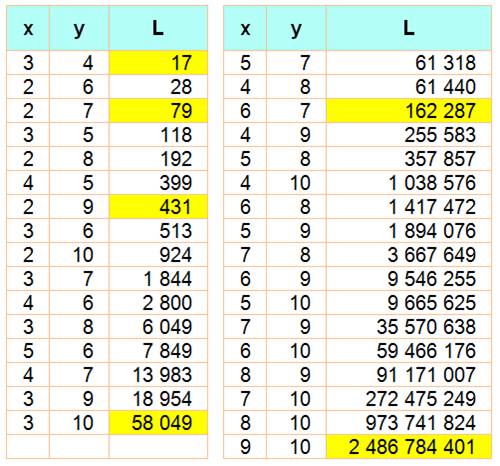
Table des valeurs
croissantes jusqu'à 20 000 000 000 (93 valeurs) L = xy
+ yx
Liste: 53 jusqu'à 107 8, 17, 32, 54, 57, 100, 145, 177, 320, 368, 512, 593, 945, 1124, 1649,
2169, 2530, 4240, 5392, 6250, 7073, 8361, 16580, 18785, 20412, 23401, 32993,
60049, 65792, 69632, 93312, 94932, 131361, 178478, 262468, 268705, 397585,
423393, 524649, 533169, 1048976, 1058576, 1596520, 1647086, 1941760, 2012174,
2097593, 4194788, 4208945, 4785713, 7861953, 8389137, 9865625, … |
|
|
|
|
|
Plus grands nombres premiers de Leyland 67635122 + 51226753 avec 25 05 0chiffres 86562929 + 29298656 avec 30 008 chiffres |
|
|
|
|||
|
Observation
Démonstration |
|
||
|
(2k)4 + (42k) |
= 16 k4 + 24k = 16 (k4 + 24 k – 4) |
||
|
|
N = n4 + 4n |
= n4 + 2 n2
2n + (2n)2 – 2
n2 2n = (n2 + 2n)2 – 2n+1
n2 |
|
|
|
(n2 + 2n)2 – 2n+1 n2 |
= ( n2 + 2n – 2n+1)/2
n ) ( n2
+ 2n + 2n+1)/2 n ) |
|
|
|
Pour n = 1, N |
= ( 12 + 21 – 21+1)/2
x 1 ) ( 12
+ 21 + 21+1)/2 x 1 ) = ( 1 + 2 – 2 ) ( 1 + 2 + 2 ) = 1 x 5 = 5 |
|
|
|
n2 + 2n – 2n+1)/2 n |
> 1 ? |
|
|
|
|
Quantité strictement supérieure à 1. |
|
|
Conclusion: |
N = n4 + 4n |
= ( n2 + 2n – 2n+1)/2 n ) ( n2 + 2n
+ 2n+1)/2 n ) |
|
Voir
Équations
diophantiennes / Formes
divisibles
|
|
||
|
32 + 23
= 9 + 8 = 17, premier premier
|
|
|
Suite (miroir) en Divisibilité
de nk + kn
![]()
|
Suite |
|
|
Voir |
|
|
Diconombre |
|
|
Site |
|
|
Cette page |
![]()