NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 02/12/2020 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	NOMBRES
Débutants Général	Dénombrement			Glossaire Général
INDEX Puissance Décomposition	Bell	Bernoulli	Motzkin	Catalan
	Parts de tarte		Genocchi
		Sommaire de cette page >>> Liste des nombres de Bernoulli >>> Application >>> Somme des puissances – Formules et valeurs >>> Fonction génératrice >>> Algorithme d'Ada Lovelace

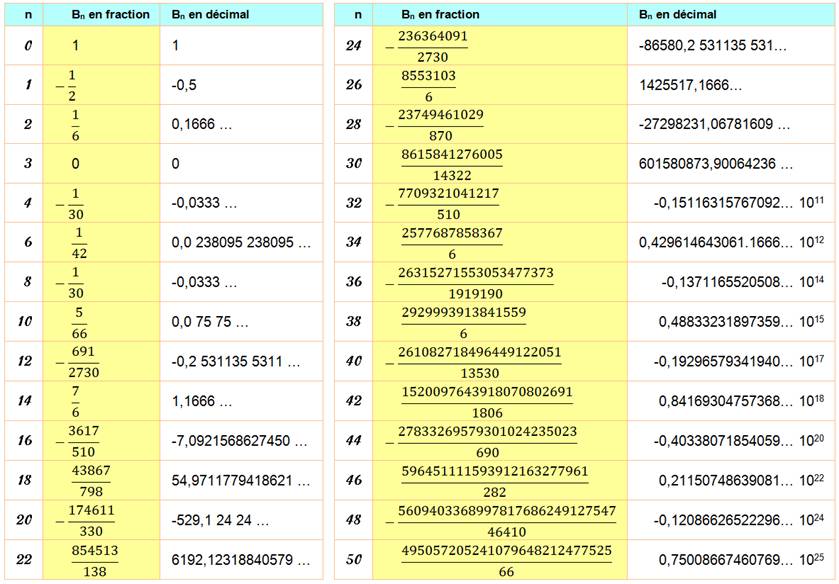
NOMBRES de BERNOULLI

Formule de Faulhaber

Nombres rationnels qui interviennent dans les problèmes de dénombrement, les calculs de somme de puissances et bien d'autres …

La famille BERNOULLI

Famille Bernoulli: suisses mathématiciens et aussi physiciens.

Jacques ou Jacob (1654-1705): épreuve de Bernoulli, nombres de Bernoulli, Lemniscate de Bernoulli, Inégalité de Bernoulli, isopérimètre, somme des puissances de 10.

Jean (1667-1748): calcul infinitésimal.

Nicolas II ou Nicolaus (1695-1726): équations différentielles, probabilités, dénombrement.

Daniel (1700-1782): théorème de Bernoulli, théorie cinétique des gaz, équation de Daniel Bernoulli.

Voir Contemporains / Vitesse du jet

Liste des nombres de Bernoulli
À partir de 3 tous les nombres de Bernoulli de rang impair sont nuls. Notez l'écriture des nombres décimaux montrant un éventuel cycle.

Applications: somme des puissances

Les nombres de Bernoulli apparaissent en tant que coefficients dans la formule donnant la somme des puissances d'ordre quelconque. On connait les formules donnant la somme des entiers, des carrés, des cubes … Bernoulli (1713) voulait une formule générale quelle que soit la puissance m. La formule existe même si elle n'est pas simple. On cherche à calculer: La formule est la suivante (formule de Fualhaber): Les deux nombres l'un sous l'autre entre parenthèses sont les coefficients du binôme (ou la quantité de combinaisons). Voir tableau ci-dessous pour développements. Même formule mais avec somme abrégée et coefficients du binôme développés: Les nombres de Bernoulli interviennent aussi dans la formule donnant la somme des inverses des puissances paires. valable pour m pair (car les Bernoulli impairs sont nuls à partir de 3) . Appliquée aux carrés (m = 2) cette formule devient:

Somme des puissances de 0 à 10

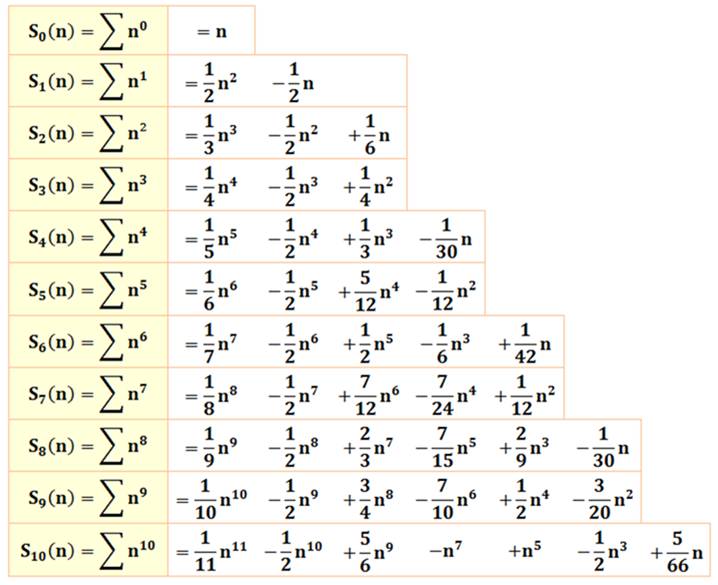
Explications Sk(n): Somme des nombres de 0 à n – 1, chacun porté à la puissance k. Ainsi, S1(n) est la somme des entiers de 1 à n avec la formule connue: S = ½ (n – 1) n. Exemple avec la somme des carrés: Calcul direct de la somme des carrés : S2(3) = 0² + 1² + 2² = 5 (n étant la quantité de nombres y compris le 0) Et, la formule ci-dessous donne bien: S2(3) = 1/3 (27) – ½ (9) + 1/6 (3) = 9 – 9/2 +1/2 = 5. Formules Attention: on compte la quantité de nombres sommés y compris le 0 Si vous voulez la somme de 1 à k faire n = k + 1 Voir Somme des puissances jusqu'à 20, formules classiques avec n Valeurs des sommes pour puissance k de 1 à 10 et nombres de m = 1 à 10 (avec m = n – 1) Exemple: 1² + 2² + 3² + 4² = 30

Voir Tables – Index

Fonction génératrice des nombres de Bernoulli
Les nombres de Bernoulli sont aussi les coefficients du développement en série de cette fonction Convergence pour . Pour les obtenir avec le logiciel Maple:

Algorithme d'Ada Lovelace
Document complet – Wikipédia

Voir Ada Lovelace et son algorithme / Les 15 plus importants algorithmes de l'histoire

Merci à Claude M. pour sa contribution

Suite	Nombres de Bell Nombres Boustrophédon
Voir	Nombres premiers réguliers Nombres tangents Formule de Stirling Somme des puissances
Diconombre	Nombre – 0,5 Autres nombres
Sites	Formule de Faulhaber – Wikipédia The Bernoulli Number Page – Bernd C. Kellner Bernoulli Number – Frank Harris
Cette page	http://villemin.gerard.free.fr/aNombre/TYPDENOM/Bernoull.htm