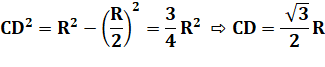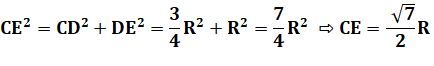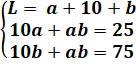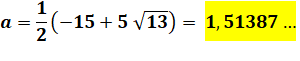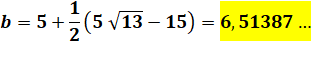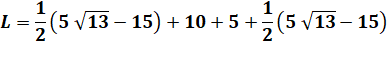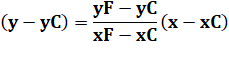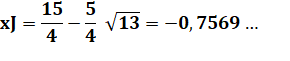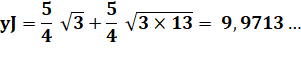|
|||||||||||||||||||||||||||||||||||||||||
![]()
|
dans le cercle Calculs Sur cette
page, à partir d'une figure relativement simple, une question de calcul de
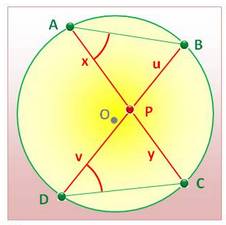
longueur qui donne du fil à retordre ! Une des méthodes
de résolution fait appel au théorème
des cordes sécantes: u
· v = x · y (Illustration =>) |
|
|
||
|
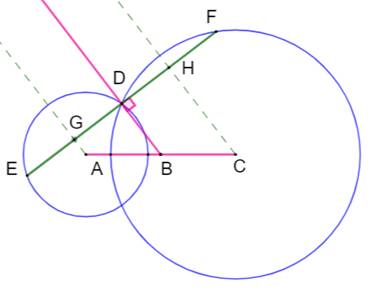
Problème Deux cercles sécants en D. Construire une sécante en D découpant deux cordes
de même longueur. Construction Milieu B de AB, segment joignant les deux
centres. Demi-droite BD. Perpendiculaire en D à BD. Intersections E et F. ED = DF. Explications Les trois parallèles AG, BD et CH découpent sur
GH la même proportion 1/2 que sur AC. GD = DH Toutes les parallèles sont perpendiculaires à EF. Les cordes ED et DF sont coupées en leur mileu. GD = DH =
> ED = DF. |
|
|
Voir Brève
900
|
|
|||
|
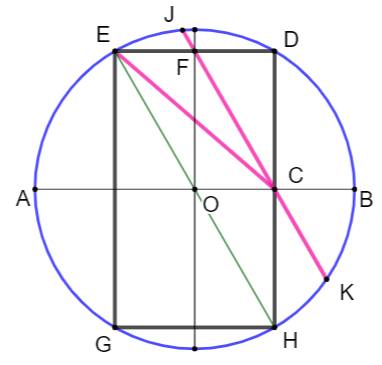
Figure Sur cette
figure, le point C est le milieu du segment OB. On prend OA = R = 10. Question Longueur
de CF, DC, CE et JK ? Longueur de CF Ce segment
est la diagonale du rectangle OCDF dont l'une des diagonales (OD) est un
rayon: CF = R = 10. Longueur de DC Théorème
de Pythagore: CD² = CF² – FD² |
|
||
|
Longueur de CE |
|
||
|
Longueur de JK |
Je propose deux solutions:
|
||
Suivi sur la figure
|
Mon astuce pour suivre les explications sur la figure consiste à recopier
la figure ci-dessus dans un autre document ou mieux de le copier avec l'outil
de capture. |
|
|
||
|
Corde JK a = JF b = CK L = JK FC = R = 10 |
Longueur de la corde: Application du théorème des cordes sécantes à JK
et ED: Application du théorème des cordes sécantes à JK
et DH: |
|
|
Système d'équations |
|
|
|
Avec différence des deux dernières |
|
|
|
La deuxième: valeur de a |
|
|
|
Valeur de b |
|
|
|
Longueur de JK = L |
|
|
Voir Équations avec somme
et produit / Astuce
de calcul avec somme et produit
|
|
||
|
Équation du cercle |
y² + x² = 100 |
|
|
Équation de la droite CF |
|
|
|
Intersection cercle et droite Calcul un peu fastidieux qui donne les solutions
indiquées. (Vive les logiciels de maths
!) |
|
|
|
Longueur de JK |
|
|
![]()
![]()