|
||||||||||||||||||||||||||||||||||||||||||
![]()
|
|
|
|
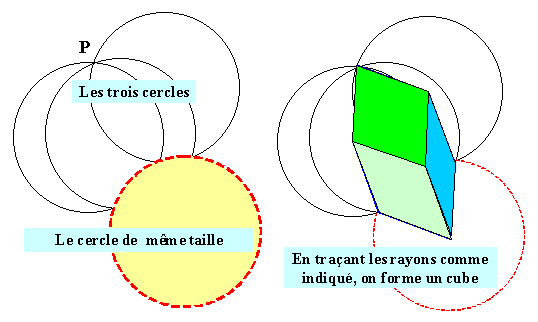
Trois cercles identiques qui passent par un point
commun: leurs trois intersections se trouvent sur un
cercle... de même taille !
|
|
|
|
|
|
Quatre cercles qui passent par un point. Les cercles qui passent par les intersections se
coupent en un point. La figure montre les 4 cercles. On dessine les quatre cercles
passant par 3 intersections (deux exemples en rouge). Les 4 cercles obtenus se coupent en un point.
Généralisation Soit n cercles qui passent par un
point: les n cercles qui passent par les intersections se
coupent en un point unique. |
|
|
|
|
|
Henri Poincaré
émet une conjecture, et George Birkhoff la démontre (1913). Hypothèses: Un anneau de matière souple limité par deux cercles.
Le cercle extérieur tourne dans un sens tandis que le cercle intérieur tourne
dans l'autre. La matière de l'anneau est déformée de manière uniforme. Théorème: Il existe au moins deux points de cet anneau qui restent au repos. |
|
![]()
![]()