|
|||||||||||||||||||||||||||||||||||||||||||||
![]()
|
Tangente du cercle Une courbe et un point. Il
existe une infinité de sécantes passant par le point. Laquelle est la plus proche
de la courbe ? Il n'y en a qu'une, la tangente. Elle touche la courbe sans la
couper. Apollonius
de Perge est connu pour ses travaux sur les coniques. Mais, il résout
aussi le problème des tangentes en imaginant de nombreuses constructions
géométriques. Newton
et Leibniz
vont revenir sur ces problèmes deux mille ans plus tard avec le calcul infinitésimal
ou calcul
différentiel. Calculs qui décrivent les courbes par l'étude des
variations des fonctions associées. Définition et constructions des tangentes du
cercle. |
|
|
||
|
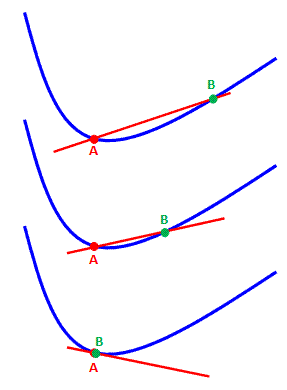
Tangente à une courbe Position limite*
d'une sécante telle que les deux points d'intersection A et B tendent
à se confondre. * lorsqu'elle
existe
Voir Courbure |
Tangente à un cercle Même définition. Propriété Le rayon aboutissant au point de tangence est
perpendiculaire à la tangente.
|
|
Voir Dérivée
/ Calcul
infinitésimal / Vitesse
|
|
||
|
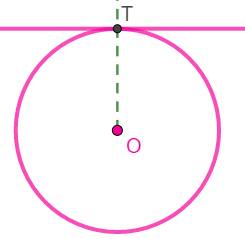
On donne
le cercle de centre O et un point A sur le cercle. Construction 1.
Tracer la demi-droite OT 2.
Perpendiculaire en T à OT. C'est la tangente. |
|
|
|
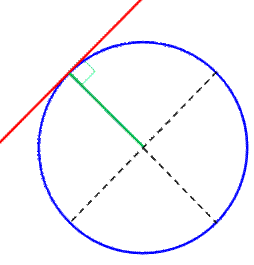
Avec construction de la
perpendiculaire 1.
Tracer la demi-droite OT 2.
Cercle (T, TO). Intersection O'. 3.
Cercles (O, OO') et (O', OO'). Intersections A et B 4.
Droite AB. C'est la tangente. |
|
|
|
|
||
|
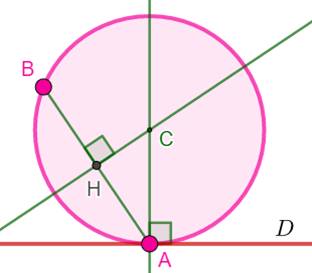
Construire
le cercle tangent à la droite D et
passant par B. Construction 1 1.
Tracer le segment AB 2.
Perpendiculaire en C à la droite D. 3.
Médiatrice de AB. Intersection
C. 4.
Cercle (C, CA). Il est tangent en A à la droite D. |
|
|
|
Construction 2 (semblable à la 1) 1.
Perpendiculaire en C à la droite D. 2.
Cercle (A, AB) et cercle (B, AB). Intersections E et F. 3.
Segment EF. Intersection C avec la perpendiculaire. 4.
Cercle (C, CA). Il est tangent en A à la droite D. Anglais: construct a circle through the
point B that is tangent to the given line at point A. |
|
|
|
|
||
|
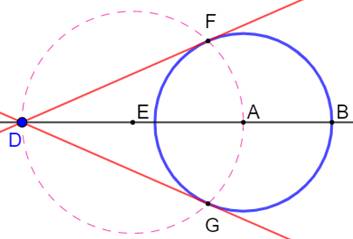
But Construire la tangente au cercle bleu à partir du
point D. Construction Point E milieu de AD. Cercle (E, EA). Intersections F et G. Ce sont les points de
tangence. Propriétés Les segments DF et DG sont égaux (isométriques). Le triangle DFA, inscrit dans un
demi-cercle et rectangle. AF est bien perpendiculaire à DF. Même chose
pour DAG. |
|
|
|
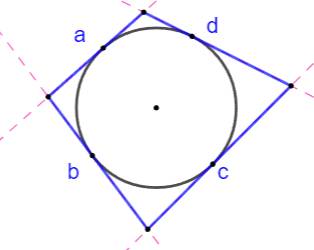
Théorème de Pitot Si un quadrilatère est
circonscriptible (c'est-à-dire si ses quatre côtés sont tangents à un même cercle),
alors la somme des longueurs de deux côtés opposés est égale à la somme des
deux autres. a + c = b + d Cette égalité découle immédiatement de la
propriété énoncée ci-dessus |
|
|
|
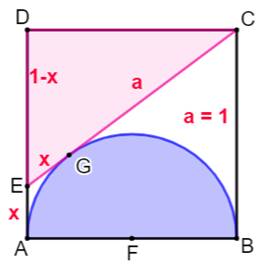
Construction Un
carré ABCD, de côté unité. Un
demi-cercle de diamètre AB. La
droite CE est tangente au cercle en G. Aire
du triangle ? Pistes (Figure
du bas) La
droite CE est tangente au cercle comme le sont les droites AD et BC. Deux
tangentes issues du même point créent des segments égaux jusqu'au point de
tangence: Calculs
Avec a = 1, l'aire vaut 3/8 (= 0,375 Scarré). |
Carré unité et ses constructions
Notations
|
|
|
|
||
|
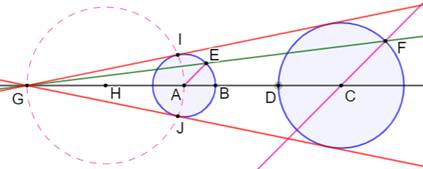
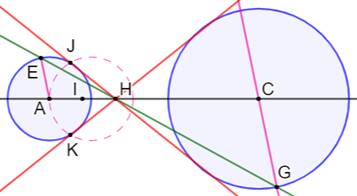
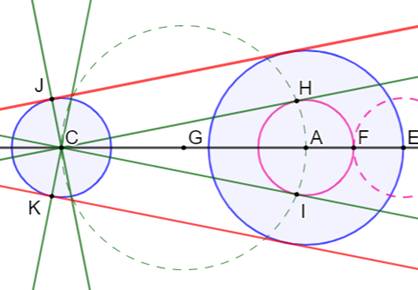
But Construire les tangentes externes
aux deux cercles bleus. Construction Point E quelconque sur un des cercles. Droite parallèle à AE en C. Point F. Droite EF. Point G. Point H milieu de GA Cercle (H, HA). Point I et J. Droites GI et GJ, les tangentes aux deux cercles. Même principe pour les tangentes internes Commentaires Avec les parallèles AE et
CF, les triangles GAE et GCF sont semblables. Ils le resteraient si on plaçait
le point E en I. Le point G est le point de
départ de la tangente aux deux cercles. Il suffit donc de tracer la
tangente au premier cercle à partir de G. |
|
|
|
Deuxième méthode via un cercle
intermédiaire Cercle rose de centre A et de rayon la différence
des rayons des cercles (FE = rayon du cercle en C). Construction de la tangente CH au cercle rose à partir
du centre C de l'autre cercle (comme ci-dessus). Perpendiculaire en C à cette tangente. Point J. Droite en J parallèle à la tangente verte. C'est
la tangente commune au deux cercles. |
|
|
|
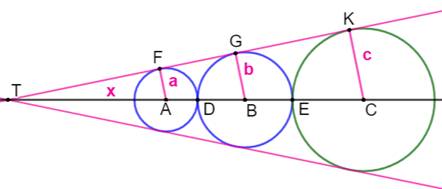
Construction Trois cercles tangent deux à deux et tous
tangents à la même droite. Connaissant le rayon des deux premiers (4 et 6),
montrez que le rayon du troisième est 9. Piste Les trois segments AF, BG et CK reliant le centre
du cercle à son point de tangence sont perpendiculaires à la tangente TK. Les trois triangles TFA, TGB et TKC sont semblables
(les trois angles sont égaux). On nomme x la longueur du segment TA. |
|
|
|
Calculs
|
||
Voir Défis simples en géométrie
![]()
|
Suite |
|
|
Voir |
|
|
Site |
|
|
Cette page |
![]()