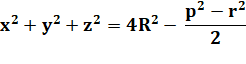|
|||||||||||||||||||||||||||||||||||||||||||||
![]()
|
CERCLES CIRCONSCRITS Avec le quadrilatère Calcul de l'aire du
quadrilatère inscriptible.
Avec le triangle quelconque Calcul du rayon du cercle
circonscrit.
Avec le triangle rectangle Il est inscrit dans le
demi-cercle et R = c/2 |
Voir Définitions
des trois types de cercles
Formulaire du quadrilatère inscriptible
|
Voir Quadrilatère
inscriptible – Approche
![]()
|
Cercle
passant par trois points Cercle circonscrit au
triangle |
|
|
|
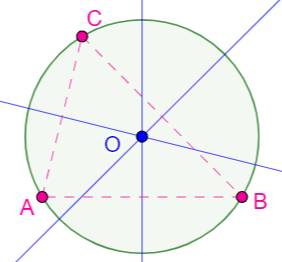
Construction Trois points quelconques A, B, C (qui peuvent
être les sommets d'un triangle). Médiatrices
des segments AB, BC et CA (bleues). Point d'intersection O qui est le centre du
cercle cherché. Centre du cercle circonscrit au triangle ABC. Le point O est équidistant des points A, B et C
et la distance est égale au rayon du cercle. Voir Médiatrices
et cercle circonscrit, calcul des coordonnées / Les
dix problèmes d'Apollonius (PPP) |
|
|
Voir Équation et diamètre d'un tel
cercle
|
Résolution d’un théorème classique du triangle
équilatéral. |
||
|
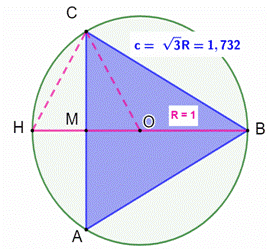
Construction
Un triangle
équilatéral ABC de côté c et son cercle circonscrit. Montrer que c
= √3 R , résultat qui figure le l'œuvre d'Euclide: Proposition
8 du Livre XIII des Éléments.
Cette figure est reprise
sur le tableau: Portrait
de Luca Pacioli (1447-1514/7) par le graveur Jacopo Barbari. Démonstration Avec HC = HO =
R, le triangle HCO est isocèle. Angles: HCB
est droit car il intercepte
un diamètre; Le triangle
isocèle HCO a un angle à la base de 60°, il est équilatéral et CH = R. Avec le théorème
de Pythagore :
|
Figure
Autre
méthode Loi
des cosinus dans le triangle BOC Avec cos(120°) = -1/2.
|
|
|
|
||
|
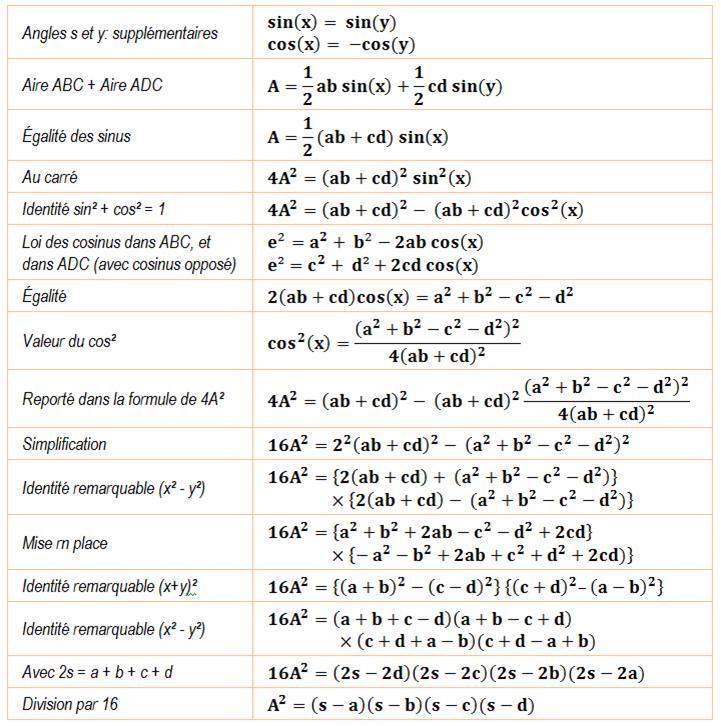
L'aire du quadrilatère inscrit dans
un cercle, en fonction de ses quatre côtés, est donnée par la formule de
Brahmagupta, une généralisation de la relation de Héron. Ce qui va servir Les
angles x et y qui interceptent la même corde AC sont supplémentaires (x + y =
180°). L'aire du triangle ABC est
connue: AABC = ½ ab sin(x). Sinus et cosinus
sont liées par sin² cos² = 1 De plus,
le cosinus dans le
triangle quelconque est connu en fonction des côtés. |
|
|
|
Démonstration
|
||
Voir Cercles
inscrits dans le quadrilatère cyclique / Identités remarquables
Exemples
|
(1,
2, 3, 4) => s = 5; A² = 24; A =
4,8989794855664… (1,
2, 3, 6) => s = 6; A = 0 |
|
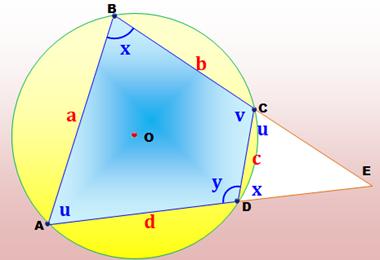
Une autre piste de démonstration Prolongez
deux côté opposés. Les triangles EBA et EDC son semblables: angle commun en E
et angles égaux valant u et x. Le
rapport des aires entre les deux est égal à (c/a)² L'aire du
quadrilatère vaut: A = T –
(c/a)² T On
calcule T, l'aire du triangle ABE avec la relation de Héron. En fait,
le calcul se révèle particulièrement fastidieux. |
Une bonne idée, mais d'une mise en œuvre
laborieuse. |
Voir Démo complète sous la référence Kala Fischbein and Tammy Brooks
|
|
|||
|
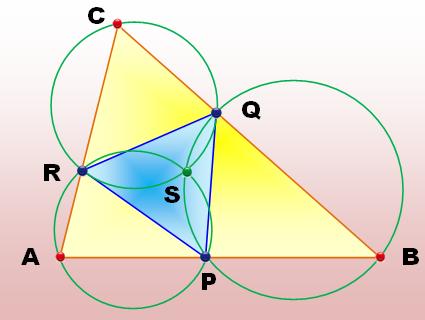
Un
triangle quelconque PQR inscrit dans un triangle quelconque (ABC), les trois
cercles circonscrits de la figure se coupe en un point unique S, le point de Miquel. ou réciproquement: Trois
cercles qui se coupent en un point définissent P, Q, R et S. Un point A
quelconque sur un cercle. AR définit C et AP définit B, alors C, Q et B sont
alignés. |
|
||
|
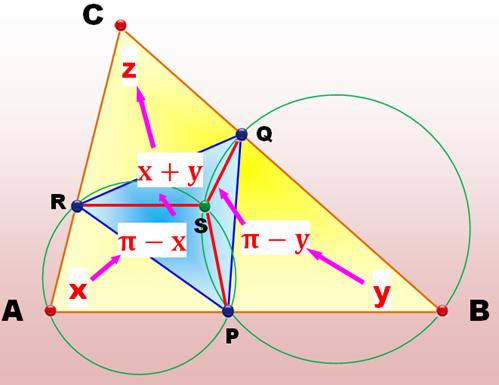
Démonstration Les deux cercles verts et les deux quadrilatères
cocycliques APSR et BPSQ. Les angles en A et B se retrouvent sous la forme
de leurs supplémentaires au centre S. De sorte que l'angle RSQ est égal à 2Pi – (Pi –
x) – (Pi – y) = x + y Dans le triangle ABC, l'angle z = Pi –(x + y),
c'est donc le supplémentaire de RSQ. Le quadrilatère du haut (CRSQ), avec ses deux
angles opposés, est cocyclique: les points C, R, S et Q sont sur le même
cercle, le fameux troisième cercle. |
|
||
Voir Les trois
cercles d'Apollonius / Théorèmes sur le cercle /
Théorème des trois
cordes / Points
remarquables du triangle
Anglais: circumradius
|
|
||
|
Un triangle
ABC. Le cercle circonscrit de centre O et de rayon R et le cercle inscrit de rayon r. Les trois perpendiculaires issues
de O. Elles sont aussi les médiatrices (formant le
lieu du centre O du cercle circonscrit). Théorème de Carnot x + y + z = R + r Démonstration Du fait des angles droits en D et E, les points
CDOE sont cocycliques.
Idem pour les deux autres cas. |
|
|
|
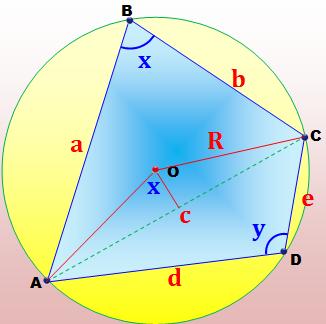
Théorème de
Ptolémée pour les quadruplets cocycliques : |
½ bx + ½ ay = ½ cR |
|
|
Aire
du triangle ABC de deux manières différentes et égalités des aires. |
A = ½ (a
+ b + c ) r = s . r A =
A(AOB) + A(BOC) + A(COA) = ½ (cz + ax + by) |
|
|
Somme des quatre relations (en simplifiant les ½) |
bx + ay
+ bz + cy + az + cx + cz + ax + by = (a + b
+ c) R + (a + b + c ) r |
|
|
Factorisation en remarquant que : |
(a + b +
c) (x + y + z) = ax + ay + az + bx+ by+ bz + cx+ cy +
cz |
|
|
Calcul et simplification (car a + b+ c est
différent de 0) |
(a + b
+ c ) (x + y + z) = (a + b + c) R + (a + b + c ) r x + y
+ z = R + r |
|
|
|
||
|
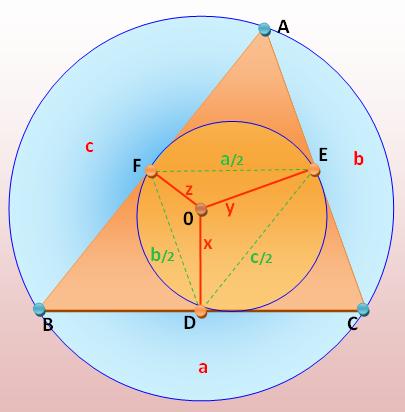
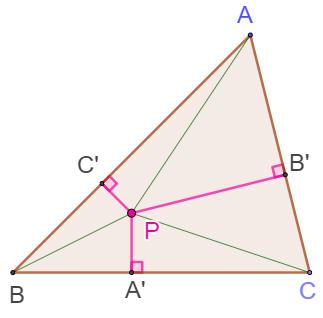
Un triangle ABC. Un point P et sa projection sur
les côtés en A', B' et C' . Le triangle A'B'C' est le triangle pedal
par rapport au point P. Théorème de Carnot BA'² – A'C² + CB'² – B'A² + AC'² – C'B² = 0 Démonstration Application du théorème
de Pythagore: |
|
|
Lazare Carnot (1753-1823)
|
Il publie Géométrie de position en 1803, ouvrage dans
lequel figure ce théorème. Un de ses deux fils, Sadi
Carnot (1796-1832) le physicien est l'un des pères de la thermodynamique
et du moteur thermique. |
Voir Contemporains
|
|
||
|
Le
sagittas sont les segments sur les médiatrices situés entre le cercle
circonscrit et le triangle. Avec p le
semi-périmètre: On a:
|
|
|
|
|
||
|
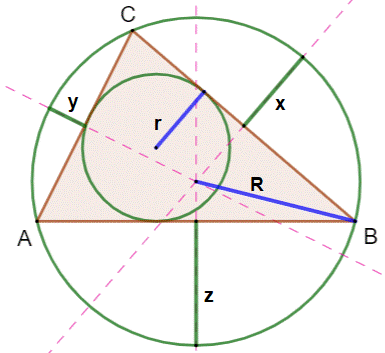
Construction Un triangle isocèle ABC. Son cercle inscrit (rose). Son cercle circonscrit –bleu). Le cercle vert est tangent au cercle circonscrit
et aux côtés AB et BC du triangle. Propriété Le milieu O des points de tangence I et J est le
centre du cercle inscrit. Démonstration (piste
pour les cracs) En utilisant l'homothétie
de centre B qui transforme K en O … Elle transforme D en K. |
|
|
![]()
|
Suite |
|
|
Voir |
|
|
|
|
|
Cette page |
![]()