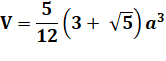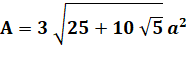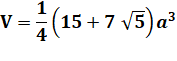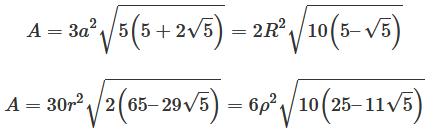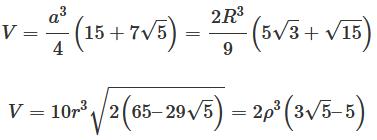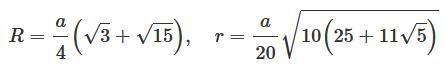approximation de la sphère

NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 30/03/2011 Orientation générale DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique
	SOLIDES
Débutants Géométrie	Approcher la SPHÈRE		Glossaire Géométrie
INDEX GÉOMÉTRIE	Sphère	Proche
		Sommaire de cette page >>> Polyèdres réguliers >>> Autres polyèdres >>> Remplissage de la sphère >>> Ballon de football

POLYÈDRES PROCHES de la SPHÈRE

Comment approximer la sphère par un volume polyédrique ?

Comment choisir le volume pour construire un ballon de football ?

POLYÈDRES RÉGULIERS

proches de la sphère

ICOSAÈDRE

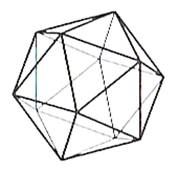
L'icosaèdre, un des cinq solides platoniciens, est un polyèdre régulier qui se rapproche de la sphère.

Il est formé de:

20 faces triangulaires,

12 sommets,

30 arêtes,

20 + 12 = 30 + 2 (relation d'Euler).

Aire et volume, avec a la longueur de l'arête:

Angl. Icosahedron

DODÉCAÈDRE

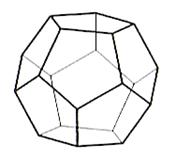
Le dodécaèdre, un des cinq solides platoniciens, est un autre polyèdre régulier qui se rapproche de la sphère.

Il est formé de:

12 faces pentagonales,

20 sommets,

30 arêtes,

12 + 20 = 30 + 2 (relation d'Euler).

Aire et volume, avec a la longueur de l'arête:

Angl. Dodecahedron

Propriétés

L'icosaèdre et le dodécaèdre, placés à l'intérieur de la même sphère, ont aussi la même sphère inscrite.

Le triangle de l'icosaèdre et le pentagone du dodécaèdre sont inscrits dans un cercle de même taille.

Le ratio des volumes pour ces deux objets est le même que celui des aires.

AUTRES POLYÈDRE

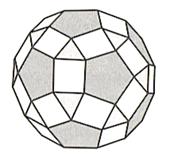
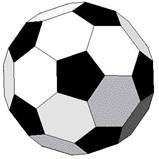
ICOSAÈDRE TRONQUÉ

L'icosaèdre tronqué est un polyèdre archimédien semi-régulier formé de:

32 faces

12 pentagones,

20 hexagones,

60 sommets,

90 arêtes,

32 + 60 = 90 + 2 (relation d'Euler).

La molécule de buckminsterfullerène, formée de 60 atomes de carbone, a la structure de l'icosaèdre tronqué.

Diamètre de la molécule: 1 nm (10^-9 m).

Découverte 1985.

Carbone pur: C₆₀

Fullerène, du nom de Richard Buckminster Fuller.

Angl. Truncated icosahedron, , football ball, soccer ball,

fullerene molecule, buckyball

Alle. Trunkatiertes Ikosaeder

RHOMBICOSIDODÉCAÈDRE

Le rhombicosidodécaèdre est un solide archimédien formé de:

62 faces triangulaires,

20 triangles,

30 carrés,

12 pentagones,

60 sommets,

120 arêtes,

62 + 60 = 120 + 2 (relation d'Euler).

Angl. rhombicosidodecahedron, or small rhombicosidodecahedron

REMPLISSAGE de la SPHÈRE

Polyèdres réguliers	Taux
Tétraèdre	12, 2518 %
Cube	36, 7553
Octaèdre	31, 8310
Icosaèdre	60, 5461
Dodécaèdre	66, 4909
Polyèdre semi-régulier
Icosaèdre tronqué	86, 74
Icosaèdre tronqué, ballon de foot gonflé	95
Rhombicosidodécaèdre	94, 32

Remarque

L'icosaèdre remplit moins bien la sphère que le dodécaèdre.

Pourtant, visuellement il semble plus proche de la sphère, c'est que

il a plus de faces et

ses angles sont moins saillants.

C'est pourquoi l'icosaèdre, avec un supplément d'adoucissage (troncature), s'est trouvé élu comme volume approprié pour construire le ballon de football.

Le rhombicosidodécaèdre, qui semble encore mieux, n'a pas été retenu car plus difficile à fabriquer; il faut faire 120 coutures au lieu de 90 pour l'icosaèdre tronqué.