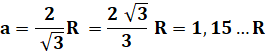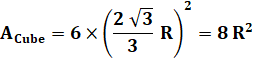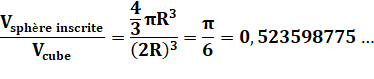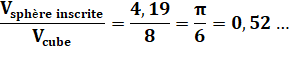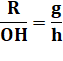|
||||||||||||||||||||||||||||||||||||||||
![]()
|
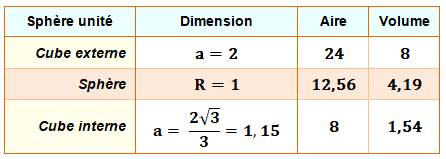
Sphère, cube et octaèdre Sphère inscrite et sphère
circonscrite Le tableau montre l'aire et le
volume de la sphère,
du cube
et de l'octaèdre. Il indique le rayon de la sphère
inscrite ou circonscrite au cube ou à l'octaèdre. Le calcul détaillé fait
l'objet de cette page.
Exemple de lecture:
pour un cube de côté unité: la sphère interne (inscrite) aura un rayon de a/2
et la sphère externe (circonscrite) aura un rayon égal à racine de 3 sur 2 =
0,866 ... Même chose pour l'octaèdre de côté unité et les deux sphères. |
|
|
|||
|
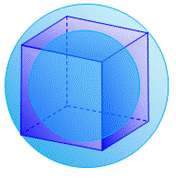
Sphère circonscrite (cube à l'intérieur) Le
cube inscrit
dans la sphère est tel que chaque sommet est en contact avec la sphère. La
distance du centre à tout point de la sphère est R; c'est également la
longueur de l'arête du petit cube jaune. Le cube inscrit, le grand, à droite,
comprend huit petits cubes. Calcul Le
rayon R du cercle circonscrit
est égal à la grande diagonale d'un cube de côté a:
Si
la sphère a un rayon R, quel est la longueur L côté du cube inscrit ?
Comparaisons Volumes
Aires
|
Cube à l'intérieur:
inscrit dans la sphère ou sphère circonscrite au
cube.
|
||
|
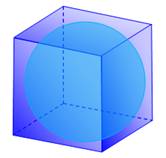
Sphère inscrite (la sphère est à l'intérieur) La
sphère est en contact avec chaque face du cube (point de tangence). Une
coupe passant par le centre montre que le côté du carré vaut 2R. En
effet, le cercle en rotation autour d'un de ses diamètres engendre la sphère
qui reste contenue dans le carré. Dimensions Aire
du cube: 6a² = 6 x 2² = 24 Volume
du cube: a3 = 23 = 8 |
Cube à l'extérieur: cisconscrit à la sphère ou sphère inscrite dans le
cube. |
||
|
Récapitulatif
|
|
||
|
|
|
||
|
Cas du cube et Soit une sphère de rayon R, elle occupe 52 % du volume du
cube qui l'enveloppe (son côté vaut 2R). |
Avec les formules
Avec les valeurs numériques du tableau ci-dessus
Certains voient une
relation entre ce rapport et la coudée
royale égyptienne
qui vaut entre 52 et 54 cm. |
||
Merci à François-Joseph pour ses commentaires
|
|
||
|
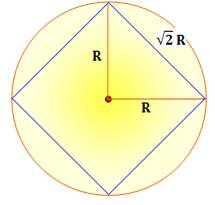
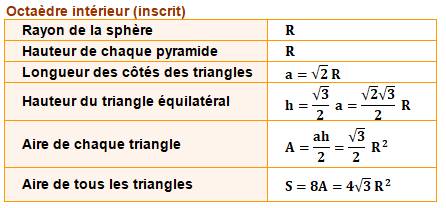
Un
octaèdre
est formé de deux pyramides à base carrés dont les
faces sont 2x4 = 8 triangles équilatéraux. Sphère circonscrite (Octaèdre à l'intérieur) La hauteur de la
pyramide est égale à R. La base est le carré
inscrit dans le cercle. Son coté vaut:
C'est le côté des
triangles équilatéraux dont la hauteur vaut: Rayon de la sphère
circonscrite:
|
|
|
|
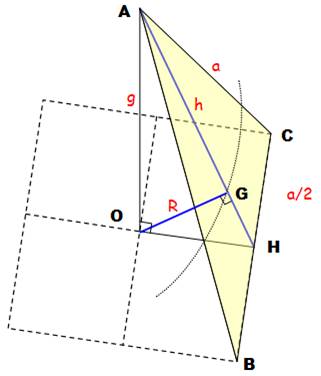
Sphère inscrite (sphère à l'intérieur) Cette fois la sphère
est en contact avec les faces des triangles. Une coupe verticale
qui partage l'octaèdre en deux avec CA et CB les hauteurs de deux faces
opposées. Calcul de R Dans le triangle
isocèle-rectangle OAC: Dans la face ABC
(triangle équilatéral), la hauteur vaut: Les triangles
rectangles OAH et GOH sont semblables: Soit la valeur de R:
|
|
|
|
Pour une sphère de rayon unité Le
tableau montre l'encadrement en aire et en volume par l'octaèdre circonscrit
ou inscrit. Avec:
|
|
|
![]()
|
La
sphère occupe en gros la moitié du cube qui l'enveloppe. |
Voir Sphère et
cylindre
|
|
|
|
|
|
À volume V égal, lequel des eux a la plus petite surface A (aire)? Comparaison
La surface du cube dépasse de 24% celle de la sphère. |
|
Devinette: balle, disque et anneau
|
La
balle, le disque et l'anneau ont le même diamètre. Sans
effet particuliers ni frottements, quel est l'objet qui roule le plus vite
sur un plan incliné? La
balle a moins d'inertie angulaire, elle a moins de masse en périphérie; elle
roule le plus vite. L'anneau
a une masse répartie en périphérie, il roule le plus lentement. Il a une plus
grande résistance inertielle. Souvenez-vous
du patineur. Il tourne plus vite les bras le long du corps. |
![]()
|
Suite |
|
|
Voir |
|
|
DiciNombre |
|
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/Geometri/Sphecube.htm
|
![]()