|
|||||||||||||||||||||||||||||||||||
![]()
|
NOMBRES HAUTEMENT COMPOSÉS et quantité de diviseurs Un nombre est hautement composé s'il a plus de diviseurs que pour tous ceux
qui le précédent. La fonction arithmétique tau ( |
Anglais:
Highly composite number or antiprime
Table des nombres hautement composés et quantité de diviseurs
jusqu'à 10 millions
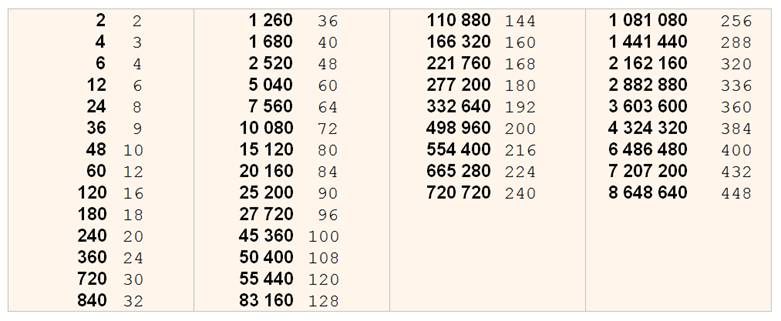
Suite de la table avec factorisation
Curiosité esthétique: notez la forme des nombres à partir
de 720
720.
"Cousins" très composés (autant que le hautement
composé 720 720)
|
Hautement composés et primorielles
|
Les
premières primorielles: 2, 6,
30, 210 Quels
sont les produits possibles: 2, 2 x 2 = 4,
2 x 6 = 12, 2 x 30 = 60, 2 x 210 = 420 6, 6 x 30 = 180,
6 x 210 = 1 260 30, 30 x 210 =
6 300 Les
nombres hautement composés sont tous produit de primorielles. Réciproque non
valable. |
|
|
|
|
Observations
|
|
Table des
nombres hautement composés avec factorisation
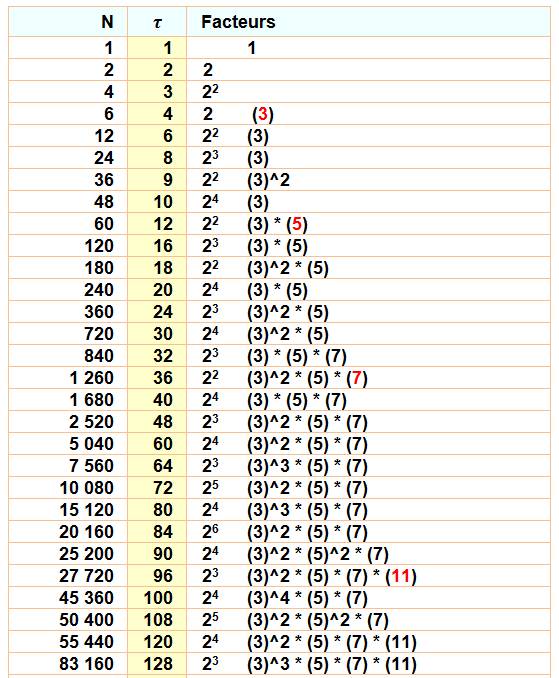

Le
nombre 5 040 a 60 diviseurs qui a 12 diviseurs qui a ….

Voir Développements
![]()
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Sites |
|
|
Cette page |
![]()



