Bases de numération, introduction

NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 01/12/2020 Orientation générale DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	BASES de NUMÉRATION
Débutants Nombres	Les BASES			Glossaire Nombres
INDEX Numération	Index bases	Introduction	Spécifique	Toutes les bases
			Maximum
		Sommaire de cette page >>> Approche >>> Table >>> Bases possibles >>> Principe de numération en base B >>> Exemple avec 1000 >>> Système unaire

Bases de numération

Introduction

Un tour d'horizon, et les détails pour chaque base en pages dédiées.

Approche

Nous savons tous compter en base 10 depuis la maternelle. Pour cela nous utilisons dix chiffres: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Lorsque nous avons compté jusqu'à 9, nous savons qu'il faut passer à 10, 11 … Ce sont les mêmes chiffres avec une position en plus. Ici les dizaines. Il s'agit de notre numération décimale dite de position.

Voir Explications détaillées

Nous aurions très bien pu ne compter qu'avec huit chiffres de 0 à 7. Alors arrivé à 7, le 8 n'existant pas, on serait passé à 10, 11, … 17, 20 … C'est la base 8 dite octale.

En base 2 ou binaire, on n'utilise que deux chiffres le 0 et le 1. Arrivé à 1, le 2 n'existant pas, on passe à 10, 11, 100 …

Pour toutes les bases inférieures à 10, on peut se débrouiller, nous disposons de suffisamment de chiffres connus.

Pour les bases supérieures à 10, il faut d'autres chiffres. On aurait pu inventer des symboles nouveaux. On convient plutôt d'utiliser les premières lettres de l'alphabet: A, B, C …

En base 12, nous utilisons les douze "chiffres" suivants: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B. De sorte que, arrivé à B, nous passons à 10, 11, 12 … 19, 1A, 1B, 20, 21 … En fait, le A en base 12 (base duodécimale), correspond au 10 en base décimale et le B correspond à 11.

Remarquez que 20 en duodécimal = 24 en décimal (deux fois la base 12).

En base 16 (hexadécimale), très utilisée en informatique, il faut utiliser 6 lettres-chiffres en plus des dix ordinaires.

Amusez-vous à composer ce tableau selon les bases de 2 à 16. Voir ci-dessous.

Tables des nombres de 0 à 26 en bases de 2 à 16

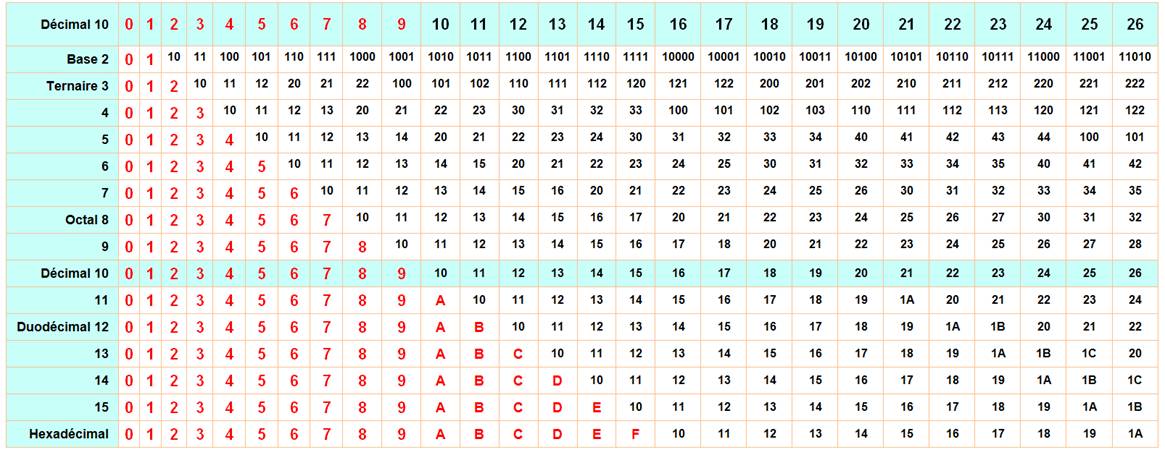
Voir Tables de conversion selon les bases

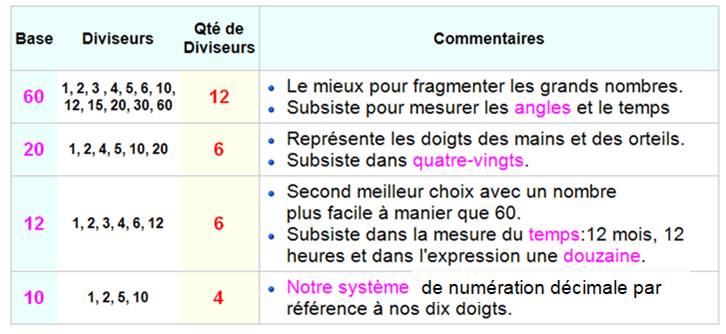
LES BASES possibles et leurs réminiscences

Voir Diviseurs / Nombres hautement composés

Principe de numération

Tout nombre entier naturel N s'écrit de manière unique comme somme de puissances de 10 pour les nombres décimaux, et puissances de B pour toute base B.
Alors:

Les coefficients a_i sont nuls ou compris entre 0 et B;

Ce sont les restes de la division par B de N, puis des quotients successifs jusqu'à ce que le quotient des divisions successives soit nul.
Remarque: si tous les coefficients sont nuls, alors N = 0; sinon le premier coefficient a₀ est différent de 0.

Avec cette écriture et dans cette base, le nombre N est unique.

Pour une base donnée, à chaque jeu de coefficients correspond un nombre unique et, réciproquement, chaque nombre se développe d'une seule telle façon avec cette base.

Exemple avec 256 en diverses bases de numération

Attention: les logiciels notent souvent les coefficients à l'envers. 256 devient [6, 5, 2].

Voir Identité remarquable / Théorème fondamental de l'arithmétique
Binaire / Octal / Hexadécimal

Merci à Gaudellycee pour ses remarques

BASES DE NUMÉRATION
Aucune	Un, deux, beaucoup	Aborigènes, peuplades reculées.
1	Unaire	Un seul symbole utilisé >>>
2	Binaire Binary	Informatique (0,1) Le chiffre prend le nom de BIT.
3	Ternaire (Trinaire) Ternary	Ternaire classique avec les symboles (0, 1 et 2). Le bit devient trit (trinary digit). Ternaire balancé avec (-1, 0, 1) qui rappelle la relation de comparaison ternaire (<, =, >). La logique ternaire utilise les trois états: (vrai, faux, inconnu).
4	Quaternaire Quaternary
5	Quinaire Quinary	Existe encore en Afrique (peul, serène...), Amérique (nahuatl, otomi...), Océanie (houailou), Asie (khmer). Au Sénégal, en lange wolof, on compte: un, deux, trois, quatre, cinq, cinq-un, cinq-deux, cinq-trois, cinq-quatre, dix, dix et un, dix et deux, etc. Les Grecs anciens utilisaient ce système: pour décrire leur manière de compter, ils disaient "cinquer". Plus d'info sur le site (K)am~itié
6	Sénaire Senary
7	Sépténaire Septenary
8	Octale Octal	Informatique En fait lecture plus commode du binaire par paquets de 3 bits
9	Nonaire Nonary	Utilisé pour compacter le système ternaire
10	Décimale / Dénaire Decimal / Denary	Quasi – universel. Avec des restes d'autres bases comme le quatre-vingts français. Mais d'autres systèmes cohabitent Corée et Japon.
11	Unidécimale Undécimal
12	Duodécimale Dudecimal	Unités de mesures en Angleterre.
13	Tridécimale Tridécimal
14	Tétradécimale Tetradecimal	Nous avons échappé à cette base car en sortant de l'eau les premiers animaux terrestres avec sept doigts.
15	Pentadécimale Pentadecimal
16	Hexadécimale Hexadecimal	Informatique. En fait lecture plus commode du binaire par paquets de 4 bits.
18	Octodécimale Octadecimal	Nombres premiers Propriété en mod 90 et en utilisant les racines numériques.

20	Vicésimale / Vigénaire ou vigésimal Vigesimal / Vigenary	Reste dans système de numération français (héritage celtique): *quatre-vingts. Reste en anglais avec le mot score*: three scores and ten = 70.
24	Tétravigésimale	Avec 12. 24 heures.
28	/	Nous comptons sur nos doigts jusqu'à dix. En comptant avec nos phalanges nous compterions jusqu'à vingt-huit. 2 fois ( 3 x 4 doigts + 2 x 1 pouce).
32	Duotrigésimlae	Avec base 16.
36	Hexatrigésimal	Base qui utilise tous les chiffres et les lettres de l'alphabet: 0, 1…9, A, B … Y, Z. Ainsi: Z₁₆ = 35_{10 et} 10₃₆ = 36₁₀.
40	Quadragésimale	Avec 20.
60	Sexagésimale Sexagesimal	Utilisé pour les angles, le temps... Origine Babylonienne
64	Tétrasexagésimale	Avec bases 16 et 32.
96	Hexanonagésimale	Avec bases 16, 32 et 64
100	/	L'Hindi, est bien en base 10, mais tous les nombres de 1 à 100 ont un nom.
144	Centetétraquadragésimale	Avec 12 (144 = 12²).
240	/	Système monétaire introduit par Charlemagne puis adopté par les Britanniques: 1 livre = 20 shillings et 1 shilling = 12 pence; soit 1 livre = 240 pence.
360	Trecentosexagésimale	Avec base 60.

Voir Énigme de Randall / Nom des polygones

n en base n

10₁₀ = 10 10 en base 10 s'écrit 10

2₂ = 10 2 en binaire s'écrit 10

8₈ = 10 8 en octal s'écrit 10

n_n = 10 n en base n s'écrit 10

n² _n = 100 le carré de n en base n s'écrit 100

n³ _n = 1000 le cube de n en base n s'écrit 1000

Etc.

EXEMPLE avec 1000

Expression de 1000 base décimale en diverses autres bases:

*Base*	*Expression de 1000*
2	1 111 101 000
3	1 101 001
4	33 220
5	13 000
6	4 344
7	2 626
8	1 750
9	1 331
10	1 000
11	8 2 A
12	6 B 4
16	3 E 8
20	2 A 0
60	[40, 16]

Au-delà de 9, il a fallu introduire de nouveaux symboles pour matérialiser les nombres nécessaires; on utilise les lettres A, B, C …
Les logiciels utilisent une notation conservant des chiffres. D'ailleurs bien utile lorsque la base est grande, comme avec 60.
Exemple: 1000₁₀ = [3,14, 8]₁₆ ou parfois inversé: [8,14,3]

Remarque: avec 1000₁₀ on a 3E8₁₆ ,

il faut aller jusqu'à 1024₁₀ pour obtenir 400₁₆ .

Système unaire ou monadique
Système unaire ou monadique (Unary numeral system) Note: ne pas confondre avec les repunits qui s'écrivent 11…1.	Système de comptage utilisé durant la Préhistoire, lorsqu'on comptait avec des cailloux, notamment pour dénombrer le cheptel. Il ne s'agit pas à proprement parler d'une base de numération (ordinal), mais d'un système de comptage (cardinal). Le symbole (ou l'objet) utilisé est écrit (ou posé) autant de fois que nécessaire (concaténation / juxtaposition). Il s'agit donc plutôt de marque de dénombrement. Ce système est encore employé lorsqu'on compte avec des bûchettes ou pour dénombrer les suffrages à un vote, etc. Un symbole quelconque représente une unité. Il n'a pas de chiffre 0, sinon avec un signe supplémentaire, ce serait du binaire. Il n'y a donc pas de façon pour représenter explicitement le rien. Applications modernes en théorie des nombres comme l'axiomatique de Peano.
Code unaire	Il existe un système de codage unaire qui utilise la convention suivante à partir d'un nombre binaire. un groupe de 0 est annoncé par un double zéro suivi d'un espace un groupe de 1 est annoncé par un zéro unique suivi d'un espace Exemple: 11011100 => 0 00 00 0 0 000 00 00 En fait, c'est un code avec deux signes: le zéro et l'espace.

Merci à Yvan Q. pour ses remarques constructives

Suite	Numération – Spécificités et bizarreries Nombres brésiliens – Repdigit en base b Autres en haut de page
Voir	Binaire Chiffres – Glossaire Tables de calculs en base 2 à 16 Romain Étymologie
Sites	Histoire des nombres et des symboles mathématiques Système unaire – Wikipédia Le chiffre – son histoire La preuve par 5 – (K)am~itié – Les systèmes de numération en appui de la paléolinguistique Base Valued Numbers Numeral & Numbers' history and curiosities. List of numeral systems – Wikipedia Names of Bases – Ask Dr. Math Numerical prefixes – The phrontisrety Notice sur les systèmes de numérations naturels: quinaire, dénaire vigénaire – M Marre
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Numerati/aaaBASE/Intro.htm