NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 19/02/2020 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Tables
Débutants Général	PUISSANCES				Glossaire Général
INDEX Tables	Puissance n	Cubes	Cubes ordonnés	Différences
	Somme des A^n	Cubes consécutifs	Cubes 2 fois
		Sommaire de cette page >>> SOMMES Nombre et puissances successives >>> SOMMES Nombres successifs et puissance

SOMMES de PUISSANCES

successives d'un même nombre

Table

Voir Somme cumulée des puissances pures

Mise en bouche –

Somme des puissances d'un nombre = puissance

Trois motifs sympathiques

3^0 + 3^1 + 3^2 + 3^3 + 3^4	= 1 + 3 + 9 + 2 7 + 81	= 121	= 11²
7^0 + 7^1 + 7^2 + 7^3	= 1 + 7 + 49 + 343	= 400	= 20²
18^0 + 18^1 + 18^2	= 1 + 18 + 324	= 343	= 7^3

Exploration jusqu'à puissance = 10 000 et un cumul des puissances jusqu'à 100

Une curiosité

7^0 + 7^1 + 7^2 + 18^0 + 18^1 + 18^2

= 1 + 7 + 49 + 343

= 400

= 20²

Le nombre 121 est le seul carré connu de la forme p⁰ + p¹ + p² + p³ + p⁴ avec p premier.

Aucun en cube jusqu'à 1 million.

Voir Pépites

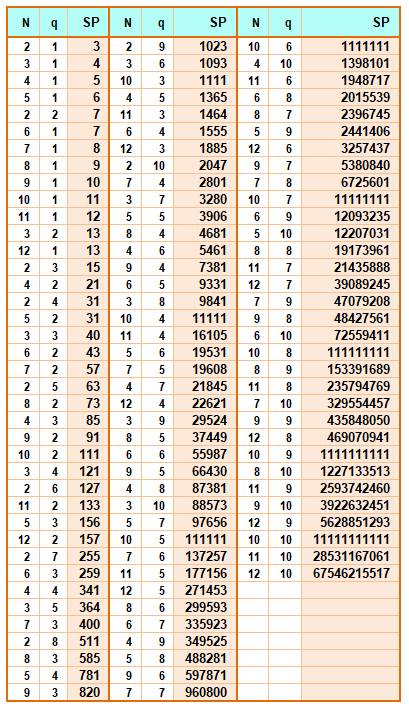
Table des SOMMES DES PUISSANCES successives d'un même nombre

par ordre croissant de la somme

Exemples de lecture de la table

2 1 3 signifie 2^0 + 2^1 = 3

2 3 15 signifie 2^0 + 2^1 + 2^3 = 15

4 4 341 signifie 4^0 + 4^1 + 4^2 + 4^3 + 4^4 = 341

C'est toujours le même nombre porté à des puissances successives

Table

SOMMES Nombres successifs et puissance

Exemples de lecture de la table

2 2 5 signifie 1^2 + 2^2 = 5

2 3 14 signifie 1^2 + 2^2 + 3^2 = 14

4 3 98 signifie 1^4 + 2^4 + 3^4 = 98

Avec le carré (2), il faut deux nombres consécutifs (2) pour avoir une somme de 5.

Ce sont les nombres successifs portés toujours à la même puissance

Table

n q SP

2 2 5

3 2 9

2 3 14

4 2 17

2 4 30

5 2 33

3 3 36

2 5 55

6 2 65

2 6 91

4 3 98

3 4 100

7 2 129

2 7 140

2 8 204

3 5 225

8 2 257

5 3 276

2 9 285

4 4 354

2 10 385

3 6 441

2 11 506

9 2 513

2 12 650

3 7 784

6 3 794

4 5 979

10 2 1025

3 8 1296

5 4 1300

3 9 2025

11 2 2049

4 6 2275

7 3 2316

3 10 3025

12 2 4097

3 11 4356

5 5 4425

4 7 4676

6 4 4890

3 12 6084

8 3 6818

4 8 8772

5 6 12201

4 9 15333

7 4 18700

9 3 20196

6 5 20515

4 10 25333

5 7 29008

4 11 39974

10 3 60074

4 12 60710

5 8 61776

6 6 67171

8 4 72354

7 5 96825

5 9 120825

11 3 179196

6 7 184820

5 10 220825

9 4 282340

7 6 376761

5 11 381876

6 8 446964

8 5 462979

12 3 535538

5 12 630708

6 9 978405

Suite	Table des Sommes de puissances successives d'un même nombre Tables avec nombres et puissances successives
Voir	Carrés – Index Puissances Cubes – Nombres Autour de 12345 Partitions en carrés Puissances et chiffres
Cette page	http://villemin.gerard.free.fr/TABLES/PuisNSom.htm