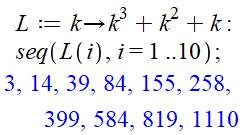|
||||||||||||||||||||||||||||||||
![]()
|
Cercles magiques Configuration
de cercles avec sommes constantes sur les circonférences. Pour les
cercles avec rayons magiques, voir les cercles
à rayons magiques |
Anglais: Magic sphere
|
Six nombres sont places sur la
circonférence d'un cercle. Pas nécessairement entiers ni distincts. Chacun est égal au produit des deux
voisins. Trouver les solutions telles que la somme
des six nombres soit un nombre entier |
|
|
||
|
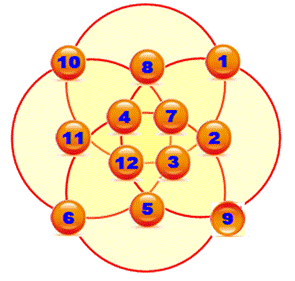
Figure
formée de k cercles qui se coupent. Les nombres sont distribués aux
intersections. La somme
des nombres aux intersections de chaque circonférence est constante. Ces cercles magiques sont présentés sur la page
Wolfram. La
constante magique vaut: k3 + k² + k Programme Maple
On définit une fonction qui associe à k, la fonction k3 + k2
+ k. On appelle cette fonction pour former une séquence de dix valeurs. |
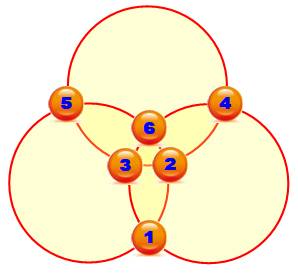
Cercle magique d'ordre 3 – Somme 14
Cercle magique d'ordre 4 – Somme 39
|
|
Voir Programmation – Index
Merci à Dr. Volker Pöhls
|
|
||
|
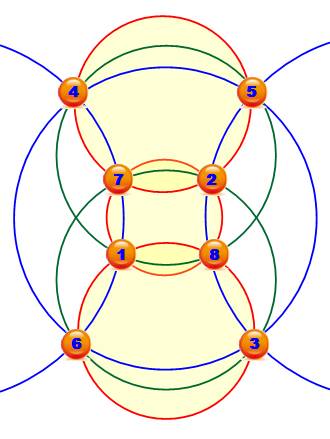
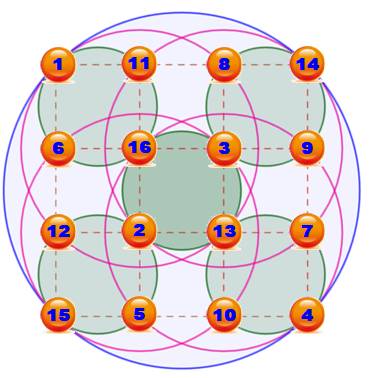
Sur
chacun des huit cercles, la somme des nombres des quatre intersections est
constante: 18. Notez que
chaque nombre est à l'intersection de quatre ercles. . |
|
|
|
|
||
|
Carré magique 4
x 4 dont la somme magique est 34. Pour un
certain nombre de carrés internes la somme des sommets vaut également 34. Ces
carrés sont repérés en dessinant un cercle qui inscrit les quatre sommets. Ce qui
produit cette jolie forme. |
|
|
|
|
||
|
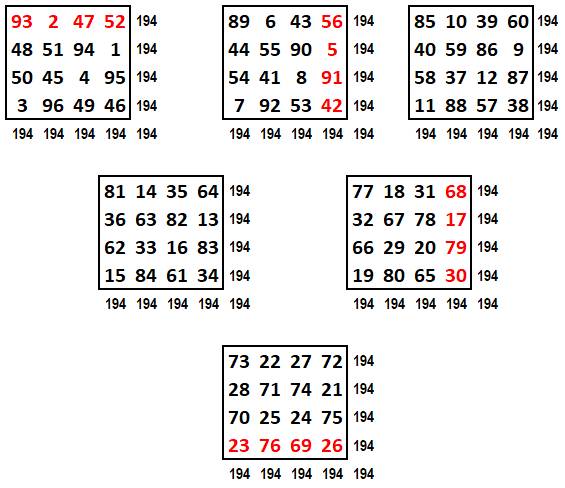
Six
carrés magiques
4 x 4 dont la somme magique est 194. La somme magique
sur les cercles est: 776 = 4 x 194. Cette figure magique est présentée sur le site très complet de Harvey Heinz. |
|
|
|
Les six
carrés magiques. Ils sont pandiagonaux. La somme
magique se retrouve 52 fois dans chaque carré. |
|
|
|
Outre la solution
triviale ne comportant que des 1, il existe deux solutions: 1,
1, 1, 1, 1, 1, s = 6 2,
1, 1/2, 1/2, 1, 2, s = 7 6,
2, 1/3, 1/6, 1/2, 3, s = 12
Solution générique: a
= bf, b = b, c = 1/f, d = 1/bf, e = 1/b et f = f. |
Voir Nombre 7 / Nombre 12
![]()
|
Suite |
|
|
Voir |
|
|
|
|
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/CarreMag/aaaCMag/Cercle.htm |
![]()