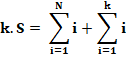|
|||||||||||||||||||||||||||||||||||||||
![]()
|
Polygones à périmètre magique Il s'agit de placer les nombres
de 1 à n sur les côtés d'un polygone
de façon que la somme
des nombres sur chaque côté soit la même. La quantité de nombres par côté est
appelée l'ordre du polygone magique. Cet exercice s'apparente à un jeu de dominos: chaque
somme est telle que le dernier terme et le premier de l'addition suivante. La somme magique étant déterminée, il s'agit de trouver toutes les partitions
de ce nombre avec les nombres de 1 à n. En 1972, Terry Trotter (1941-204) publie ses idées concernant ce type
de polygones magiques (Voir références)
Note: les solutions présentées sur cette page ont été
trouvées par ordinateur utilisant le logiciel Maple. |
Anglais: Perimeter Magic Polygons (PMP)
|
|
|||||
|
Les quatre solutions pour l'ordre 3 Il existe
quatre possibilités pour quatre sommes magiques différentes. Pour
chacun, il existe trois rotations avec le 1 prenant la place de chaque sommet
et pour chacun la possibilité de tourner dans l'autre sens. Chaque solution
possède 6 variantes. Bilan: 4 solutions de base et 24
solutions avec les rotations. Complémentaires Les
triangles de droites sont les compléments à 7 de ceux de gauche: 1 + 6 = 7, 5
+ 2 = 7, 3 + 4 = 7 … |
|
||||
|
Calcul de la somme magique On
pose les trois égalités à satisfaire et on en fait la somme. Elle
comprend la somme des
entiers de 1 à 6 et une somme variable de 6 à 15. Seules
les valeurs divisibles par 3 dans l'intervalle possible sont éligibles. |
|
||||
|
Partition et faisabilité Prenons
le cas de la somme 9. La faisabilité impose qu'il existe trois partitions
de 9 avec trois nombres de 1 à 6, tous différents. |
Parmi
les 26 partitions de 9 avec les nombres de 1 à 6, seules trois sont
éligibles. Ça tombe bien! De plus, l'enchainement "domino" existe:
153 => 342 => 261 (chacun commence par la fin de l'autre).
Avec
10, 11 et 12, il existe également trois partitions éligibles, pas plus. |
||||
|
Cas du triangle à 4 nombres par côtés: ordre 4 Contrainte: Les
cinq solutions avec le 1 au sommet Le
tableau du dessous donne les 19 solutions avec le 1 non au sommet x 6 pour
chacune des positions x 2² pour les inversions des autres côtés x 2 en tournant dans l'autre sens = 912
solutions. La somme magique se calcule comme
précédemment: Quantité de sommes magiques On
a trouvé 7 possibilités de 17 à 23 La
formule donne bien cette valeur: Notez que, d'après le tableau de droite,
les sommes 18 et 22 sont impossibles. |
|
||||
Voir Triangles – Index
|
|
||
|
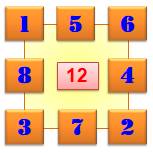
Le carré
avec 3 nombres par côtés est dit d'ordre 3. Il y a
six solutions dont celle en figure à droite:
Note: Je n'ai pas testé l'ordre 4. |
|
|
Voir Carrés
|
|
|||
|
Ordre 3 Le
pentagone d'ordre 3 possède six
solutions dont celle présentée à droite.
Notez la construction
du pentagone à somme 14:
Somme magique On calcule qu'il y a 6
possibilités de 14 à 19. On constate que 15 et 18 sont impossibles. |
|
||
|
Ordre 4 Deux exemples. On trouve les sommes: 27 = 1 + 9 + 15 + 2 = 2 + 8 + 14
+ 3 = … Notez que les deux nombres en rouge peuvent être permutés sans changer
la somme. |
|
||
|
Ordre 6 – Construction Construction
à partir de l'ordre 4 en ajoutant la même somme sur chaque côté. Pour
cela les nombres à placer sont mis par paires de même somme: Il
s'agit des dix nombres de 16 à 25. On a: 16 + 25 = 17+ 24 = 18 + 23 = 19 + 22
= 20 + 21 La
figure montre, en externe, les nombres du pentagone d'ordre 4 et en interne
(rouge) les couples ajoutés. |
|
||
Voir Pentagones / Calcul de la somme magique pour le pentagone
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Hexagone d'ordre 3 Il
s'agit de réaliser la même somme sur chacun des six côtés. Ici, à droite: 17. Deux races de solutions:
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
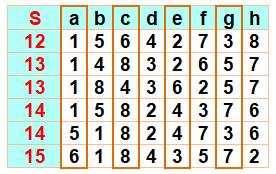
Les 40 solutions hors rotations
En
rouge le 1 au sommet; en bleu, le 1 au milieu d'un côté. En
S la valeur de la somme magique.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Voir Hexagone
et carré de Dürer / Hexagone complet magique / Hexagones
Merci à Patrick
|
|
||
|
Il y aurait 118 cas
d'heptagones à périmètre magique d'ordre 3, dont les deux présentés à
droite. Notez la construction de celui e gauche; pas toujours
aussi simple comme le montre celui de droite. |
|
|
Voir Heptagones
Voir Octogones
|
|
|||
|
k = quantité de côtés du polygone n = ordre (quantité de nombres par côté) S = somme magique (la somme sur tous les nombres
d'un côté) SS = Somme
des nombres des sommets. |
En général Il s'agit de calculer la plage de valeurs convenable pour la somme
magique de manière à concentrer la recherche de solutions. Note: la taille de la plage (quantité de sommes magiques)
pour le triangle est égal à : 3n – 5. Pour l'ordre 3, on a: 3 x 3 – 5 = 4 possibilités. |
Pour le pentagone d'ordre 4 k = 5 et n = 4
|
|
|
N = dernier nombre à placer sur le polygone |
N = k (n – 1) |
N = 5 x 3 = 15 |
|
|
Calcul sur le périmètre: on y retrouve k fois la
somme magique S. |
k.S = somme des entiers plus somme des
sommets |
5S = (1 + 2 + … + 15) + (a + d + g+ j + m) |
|
|
Somme magique minimale |
|
5S = (1 + 2 + … + 15) + (1+2+3+4+5) = 135 |
|
|
|
|
5S = ½ (15x16 + 5x6) =
135 |
|
|
|
|
S = 135/5 = 27 |
|
|
Somme magique maximale |
|
5S = (1 + 2 + … + 15) + (11+12+13+14+15) |
|
|
|
|
5S = 2 x (1 + 2 + … +
15) |
|
|
|
|
S = (2x15x16 – 10x11)
/ (2x5) = 37 |
|
|
Exemples En jaune, les trois calculs explicites effectués
sur cette page. |
|
||
![]()
|
Suite |
|
|
Voir |
|
|
Aussi |
|
|
|
|
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/CarreMag/CMgeomPo.htm |
![]()