|
||||||||||||||||||||||||||||||||
![]()
|
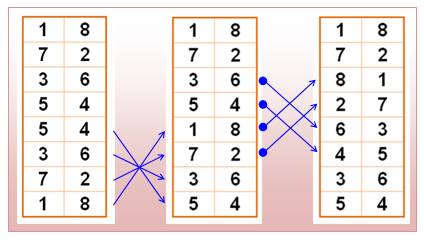
Mathématiques des Carrés Magiques La méthode de l'échelle alternée Soit un carré gréco-latin
dont les couples sont composés de nombres simplement alternés. Quel est le
résultat? On s'approche grandement d'un carré magique de Franklin. |
|
|
||
|
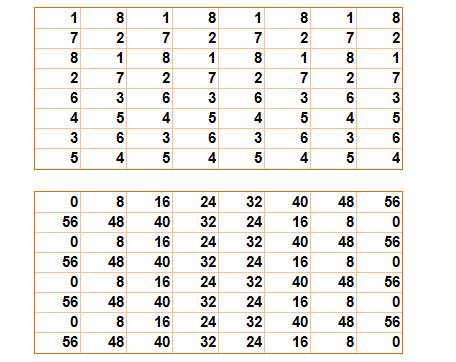
Le
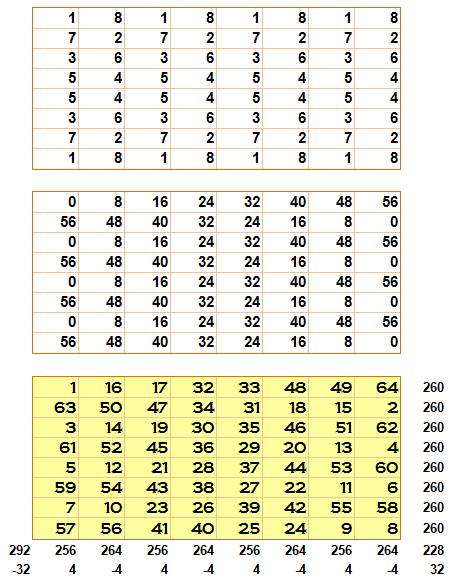
premier carré est rempli avec nombres (1, 2, 3, 4, 5, 6, 7, 8).
Le
deuxième carré est rempli avec nombres (0, 8, 16, 24, 32, 40, 48, 52).
Le
troisième carré est simplement la somme de ces deux premiers carrés: chaque
cellule est la somme des deux cellules correspondantes. |
Ce
carré magique n'est pas magique, mais s'en rapproche. |
|
|
|
|||
|
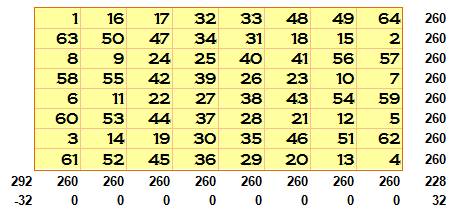
Ce carré
construit aussi simplement se rapproche d'un carré magique, ou mieux d'un carré de Benjamin Franklin. Ce carré
déroge en vertical: il faut faire la somme sur deux colonnes pour trouve deux fois la
somme magique. On se
souvient que les diagonales ne sont pas magiques dans les carrés de Franklin;
ce sont les semi-pandiagonales qui le sont. |
Lignes horizontales: 260 (8 cas)
Lignes verticales par deux: 2 x
260 (4 cas)
|
||
|
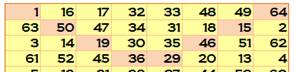
Semi-pandiagonales: 260 (96 cas) Dans ce
simple carré, on retrouve les quatre-vingt-seize cas de sommes magique sur
les semi-pandiagonales.
|
Toutes les semi-diagonales en rouge les sommes 260
|
||
|
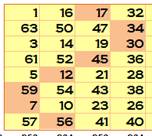
Carré 2x2 : 130 (8 x 8 cas) y compris
le carré central et la somme des quatre coins. |
|
||
|
|
|
|
Nous
venons de voir qu'il en faut peut pour obtenir un carré magique de Franklin. C'est le
cas: une simple inversion sur le premier carré va suffire. Interversions sur les deux premières colonnes du
premier carré
Les deux carrés composant le carré gréco-latin
Note: le premier tableau correspond aux restes de la
divisons par 8, alors que le second correspond aux quotients multipliés par
8. Le carré magique 8x8 de Benjamin Franklin
Note: par rapport au précédent
(presque Franklin), celui-ci a, en plus, toutes ses colonnes magiques et ses
deux diagonales qui, ensemble, donnent le double de la somme magique. |
|
Voir
Carrés de Franklin
Bilan
|
Cette méthode est
généralisable aux autres carrés de type Franklin. |
![]()
![]()