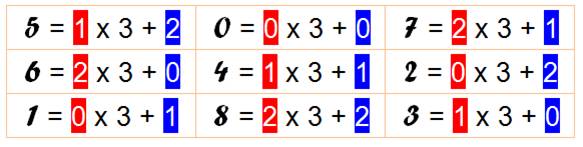|
||||||||||||||||||||||||||||||||
![]()
|
Mathématiques des Carrés Magiques La méthode d'EULER Méthode des carrés gréco-latins. Comment résoudre un carré
magique en simplifiant le problème? Euler a eu la bonne idée en 1776! Il
connaissait la méthode de La Loubière et
celle de De la Hire dont il
s'inspira. Sa méthode
Le niveau Cours Moyen (CM1
ou CM2) est suffisant pour comprendre la méthode. Les mathématiciens (niveau
avancé) utilisent ces outils pour explorer les tréfonds du monde fantastique
des carrés magiques (CM !). En bref et à retenir
Exemple
pour le premier nombre: 5 = 3 x 1
+ 2 Ça y est,
vous avec le déclic? Stupéfiant, non? Sinon,
voyons cela en détail. |
|
|
|||
|
Prenons
le plus simple des carrés magique. Le carré 3x3. On écrit
tous les nombres sous la forme de leur division euclidienne par
3, le nombre de cellules par côté. |
En maths, le carré magique est composé des nombres de 0 à n² – 1. Le
carré est dit "naturel". |
||
|
Chaque nombre est divisé par 3. On indique le quotient et le reste. Remarquez que: les couples quotient et
reste sont tous différents. |
|||
|
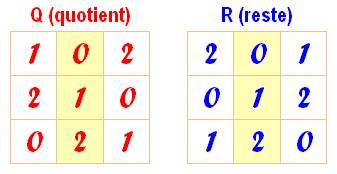
Formons
les deux carrés, l'un avec les quotients et l'autre avec les restes. La
colonne centrale est la suite des trois nombres (0, 1, 2) et les colonnes
latérales sont identiques à un décalage près. Les deux
carrés sont symétriques (colonne droite de l'un = colonne gauche de l'autre). Ils sont
magiques à leur façon: les sommes sur les lignes, colonnes et diagonales sont
égales à 3. |
Deux carrés magiques avec les nombres de 0 à 3. Ce sont deux carrés latins
orthogonaux. |
||
|
Écrire
simplifié. En maths,
on dirait que: la matrice CM3 est égale à trois fois la matrice Q plus la
matrice R. |
CM3 = 3Q +
R Carré magique d'ordre 3 = 3 fois chaque nombre du carré latin Q auxuel
on ajoute le nombre correspondant du carré latin R. |
||
|
Pourquoi
ça marche? Petites
lettres pour représenter un des nombres du tableau (matrice) et grande lettre
pour la matrice elle-même. |
1) Chaque
couple étant différent, les nombres 3q + r sont différents; et 2) Chaque
carré latin étant magique, la combinaison linéaire des deux (3q + r) est magique. |
||
Voir Propriétés du carré
magique 3x3 / Forme générique du carré magique
3x3
Bilan
|
Euler, et sans
doute d'autres avant lui, remarque qu'un carré magique d'ordre k peut
toujours se décomposer en une somme de deux matrices orthogonales:
|
|
|
|
|
Décomposition ("spectrographie") Voici, un
carré magique et sa décomposition en carrés latins orthogonaux. On se
souvient que cela veut dire simplement que les couples de nombres sont tous
différents (2,3), (1,1), (3, 2), (0,0), (3,0), … et les 16 possibles y sont
tous. Vous aurez noté que le couple (2,3) est différent du couple (3,2).
Construction Construction
d'un carré gréco latin (il est d'ailleurs
magique de somme 66). Conversion
des nombres de la base 4 vers la base 10. Le carré obtenu est magique avec
une somme égal à 30; les nombres vont de 0 à 14. Incrémentation
d'une unité dans chaque case pour passer au carré magique classique avec les
nombres de 1 à 15.
|
|
|
|
|
|
Nous
appliquons ici la méthode de construction d'un
carré latin diagonal. n = 5, a
= 2 et b = 1. De sorte que
a, b, a +b et a- b sont premiers avec n, assurant la diagonalisé du carré
latin. Ce carré
latin est transposé par ses diagonales
principales, comme si le carré était plié autour de la diagonale. Ces deux
transposées sont automatiquement orthogonales au premier. Ce sont des carrés
magiques en base 5. Une
conversion en base 10 produit les quatre carrés magiques présentés
ci-dessous. Cette
méthode marche quelle que soient la valeur de n, à condition que a, b, a +b et a- b soient
premiers avec n. Notez que cette condition est irréalisable avec n = 6.
|
|
![]()
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/CarreMag/aaaMaths/Euler.htm
|
![]()