|
||||||||||||||||||||||||||||||||
![]()
|
Mathématiques des Carrés Magiques Méthodes de construction Comment
construire un carré
magique ? Il existe de nombreuses méthodes: de la simple recette de
placement des nombres à des théories mathématiques très élaborées. Si les
premières existent de longue date, les dernières sont très récentes. Elles
bénéficient des théories mathématiques modernes avec mise à contribution des
ordinateurs Ce qui
est certain: les méthodes de construction sont différentes pour les carrés
magiques d'ordre impair (les plus faciles à réaliser) et pour les carrés
magiques d'ordre pair. Les
méthodes seront adaptées au cas de l'obtention e carrs magiques particuliers:
associatifs, panmagiques, diaboliques ou encore plus que parfait. |
Prérequis
|
Cette page est la première d'un développement sur les
mathématiques de construction des carrés magiques. On suppose que le lecteur
est familier du vocabulaire classique des
carrés magiques. |
Carrés
d'ordre IMPAIR
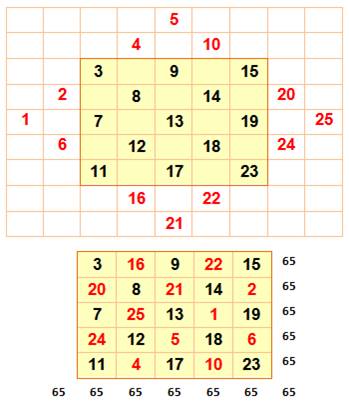
Exemple
de carré magique d'ordre 5
Les deux règles sont lustrées par les couleurs
Voir Un exemple d'ordre 9
|
Méthode
du losange, du damier crénelé, ou des terrasses Méthode
de Bachet de Méziriac |
|
|
|
Cette
méthode consiste à placer les nombres successifs sur les diagonales montantes
d'un quadrillage. Le résultat dessine un losange
de nombres. L'opération
suivante consiste à placer les nombres qui débordent à leur place équivalente, comme si le carré
s'enroulait sur lui-même. Observer
la succession des nombres. On retrouve celle indiquée dans la méthode
précédente. Voir Méthode du
losange Voir Algorithme et
programmation de cette méthode |
|
|
|
|
|
|
Méthode de Philippe De la Hire Elle
consiste à préparer deux tableaux de nombres: l'un avec les nombres de 1 à n
et l'autre avec les nombres multiples de n. Ces
nombres sont répartis dans les deux grilles de façon qu'aucun doublet ne se
ressemble. Le carré
magique est obtenu en ajoutant les nombres de chaque doublet. Exemple Aucun
doublet identiques dans les deux carrés: (4,3) est différent de (5,2), de (1,
1), etc. Ces deux carrés sont des carrés
latins orthogonaux.
|
|
|
Méthode d'Euler et méthodes
modernes Elles
s'inspirent de la méthode précédente en la généralisant. Pour des raisons
pratiques, les mathématiciens préfèrent utiliser les carrés avec les nombres
de 0 à n² -1 plutôt que de 1 à n², simplifiant ainsi les formulations. Avec
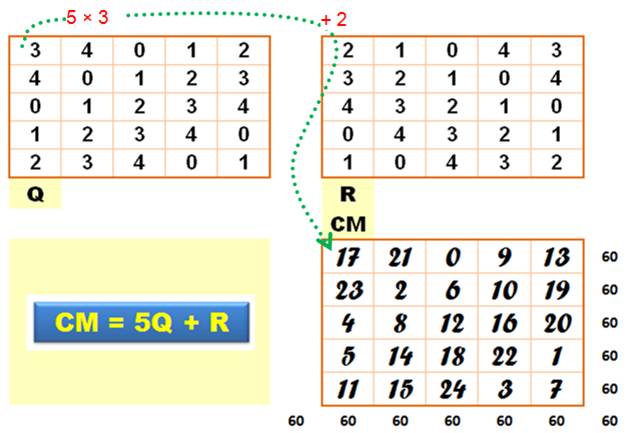
cette méthode la formation se résume à une équation matricielle. Exemple Les deux
carrés latins vus ci-dessus, décrémentés de 1. Les deux nombres de cellules en même position forment un doublet. Chaque
nombre du carré magique est égal à 5
fois le premier nombre du doublet ajouté au second.
La
notation Q et R fait référence au fait que, par exemple, 17 = 5 x 3 + 2 avec 3 le quotient
(Q) et 2 son reste (R). Q est donc la matrice
des quotients et R la matrice des restes (des modulo 5) Voir Méthode matricielle
d'Euler Carrés latins et carrés magiques |
Carrés
d'ordre PAIR
|
|
|||
|
Carré magique 4x4 Les
nombres sont placés naturellement dans la grille: de gauche à droite et de
haut en bas. Le centre
et les sommets restent en place (autrement-dit: les diagonales ne sont pas
touchées). Par
contre, les nombres latéraux sont complémentés à 17 (ou autrement-dit: chacun
prend la place de son symétrique par le centre). C'est le
plus petit carré pair et il est associatif. |
|
||
|
Principe général Pour les
ordres plus grands, les choses se compliquent. Ce schéma aide à définir la
stratégie pour la modification des placements. Les
nombres sont placés en mode serpentin. En marron foncé, les cases sur la
bonne ligne et sur lesquelles on va
s'appuyer. Les
trajets fléchés indiquent les nombres à compléter sur les lignes déjà partiellement produites
dans le sens indiqué par la flèche. Voir Construction
du carré 6x6 |
Cette présentation est utile pour la construction des carrés
magiques d'ordre pair. Le principe consiste à établir des chemins (lignes
brisées fléchées) tels que la somme sur le trajet est magique. |
||
Construction génétique
|
Il s'agit d'une
méthode de construction des carrés magiques utilisant des algorithmes
génétiques. On crée une série de carrés remplis au hasard. À chacun est attribuée
une note reflétant la "distance" au but. Les plus proches sont
reproduits en y introduisant des mutations aléatoires. L'opération est
répétée jusqu'à satisfaction: la création d'un vrai carré magique. |
Voir
gigogne pour les pairs >>>
Méthode
des diagonales (8x8)
Méthode du carré magique plus que
parfait
méthode serpentine (déjà traité qque
part)
Phéru pour les impairs
![]()
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/CarreMag/aaaMaths/Construc.htm
|
![]()