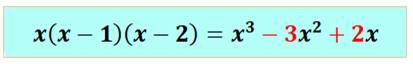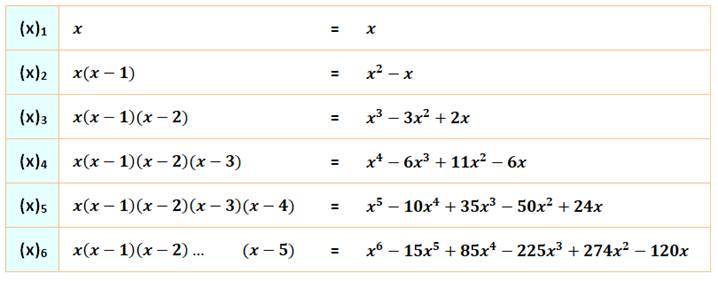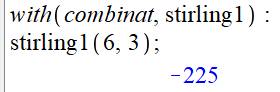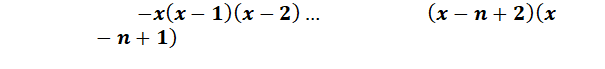NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 25/09/2023 Orientation générale  DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique Brèves de Maths
	COMPTER - Combinatoire
Débutants Dénombrement	FACTORIELLES				Glossaire Combinatoire
INDEX Compter Dénombrer	Index factorielle	Introduction		Tronquées	Généralisées
		Alternée	Tables des tronquées		Sous-factorielle
		Somme = 1/2	Nombres de Stirling 1		Stirling 2
		Sommaire de cette page >>> Factorielles tronquées de n à n – 5 >>> Mécanisme de création des nombres de Stirling >>> Valeurs des nombres de Stirling >>> Programmation >>> Différence finie des factorielles tronquées généralisées

FACTORIELLE TRONQUÉE

Nombres de Stirling

(première espèce)

Nombres multi-proniques ou multi-oblongs

Soit la factorielle tronquée de n à n – k, il s'agit d'observer les coefficients du polynôme développé.

Exemple:

Les coefficients –3 et +2 sont des nombres de Stirling.

On retrouve, ici, une nouvelle race de nombres semblables à ceux du triangle de Pascal.

Anglais: Generalized factorials: n factors, each one less than the preceding

Voir Nombre multi-pronique et leurs propriétés

Factorielles tronquées de n à n – 5
Calcul des expressions développées des six premiers polynômes. La notation classique est (x)n pour les expressions signées telles qu'exprimées dans le tableau. La notation (x)^n correspond à la même expression avec somme des valeurs absolues des termes. Chaque coefficient est noté s(n,k). Ainsi s(4,2) = 11 (on compte à partir de la droite).

Voir Identités remarquables

Mécanisme de création des nombres de Stirling

Cas de x(4!) Comment, par exemple, passer de x^3 – 3x^2 + 2x à x^4 – 6x^3 + 11x^2 – 6x. Il s'agit de multiplier la première expression par x – 3. Le schéma montre que chaque nouveau coefficient est égal à la somme du précédent augmenté de 3 fois celui qui est au-dessus. Cas de x(5!) Appliquons le mécanisme en se souvenant que les signes sont alternés: (x)5 => (1, 1x4+6, 6x4+11, 11x4+6, 6x4) (x)5 = x^5 – 10x4 + 35x^3 – 50x^2 + 24

Valeurs des nombres de Stirling (de première espèce)
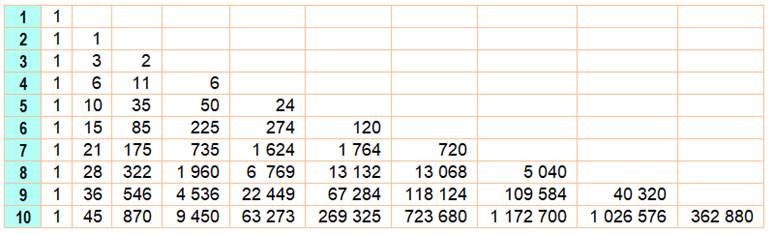
Suite des 50 premiers nombres Nombres de Stirling en situation jusqu'à x(20)

Programmation (Maple)
	Commentaires Écriture d'une procédure de calcul des coefficients de la ligne suivante connaissant une ligne (L) et le rang de la ligne suivante (k). Ls est une liste qui contiendra la ligne suivante. LL est une liste temporaire égal à L avec un 0 en début et un 0 en fin. La boucle calcule les nouveaux coefficients (c) du premier au dernier, de la même manière. Une fois la liste Ls complète elle est proposée en sortie de procédure (return) Le programme principal est initialisé avec la première liste (L) et on ouvre un ensemble vide (E) destiné à recevoir un exemplaire de chacun des nombres de Stirling. Calcul des lignes (L) de coefficients pour x(1) à x(20) et mise à jour de l'ensemble E des nombres de Stirling. On imprime au choix les lignes de coefficients L ou, en fin de programme, la liste ordonnée des nombres de Stirling (ici les 20 premiers).
	Utilisation du package Maple Maple possède les instructions toutes faites.

Voir Programmation – Index

Différence finie des factorielles tronquées généralisées
La différence finie première s'apparente à une dérivée.

Application

Les nombres de Stirling de première espèce trouvent une application majeure dans le décompte des cycles de permutations.

Par exemple, avec quatre éléments se développent quatre types de cycles avec les quantités: [6, 11, 6, 1], la ligne 4 du tableau des nombres de Stirling.

Retour	Factorielles tronquées
Suite	Nombres de Stirling de deuxième espèce Somme et produit de 3 nombres consécutifs Division des factorielles tronquées Factorielle tronquée = carré? Factorielles généralisées Produit de k nombres consécutifs – Divisibilité
Voir	Coefficient du binôme Constante "e" Constante "pi" Factorielles divisées Loto Partition en nombres consécutifs Programmation du calcul des factorielles Théorie des nombres – Index
Sites	Nombres de Stirling – Wikipédia OEIS A008275 – Triangle read by rows of Stirling numbers of first kind, s(n,k), n >= 1, 1<=k<=n. OEIS A008275 – Triangle of Stirling numbers of first kind, s(n, n-k+1), n >= 1, 1 <= k <= n.
DicoNombre	Nombre 3 Nombre 6 Nombre 10 Nombre 11	Accès à tous les Nombres
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Compter/Stirling.htm