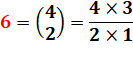|
Édition du: 13/07/2025 |
|
Dictionnaire des Nombres |
||||||||||||
|
100 / 200 |
||||||||||||
![]()
|
|
Nouvelle
orthographe avec
des traits d'union partout |
|||
|
Voir Partitions |
||||
|
|
|
Parfait
(le plus petit) Préfixes
diviseurs et multiplicateurs: 10-6 micro 10 6 méga (million) Voir |
||
Rappel
Propriétés générales >>>
|
Six ails ou six aulx.
|
Démonstration
que sin(x) / n = 6 vue
par une "blonde":
|
Voir Pensées
& humour / Alphabet parlant
/ Fractions
illicites
![]()
PROPRIÉTÉS MATHÉMATIQUES
générales
|
|
||
|
|
||
|
|
||
|
de ses diviseurs propres: il est PARFAIT. |
||
|
|
||
|
Nombre central d'une ligne du triangle
de Pascal.
|
||
|
ont une complexité inférieure au nombre. |
||
|
|
||
|
|
||
|
|
||
|
|
||
|
|
||
|
|
||
|
|
||
|
|
||
|
|
||
|
|
![]()
Chiffres
et numération
|
6 = six |
|
|
|
6 |
|
|
|
6
|
|
|
|
|
|
|
Addition
Diagramme de Ferrers du nombre 6

Voir Diagramme
de Ferrers
|
6 =
1 + 2 + 3 = 6 = 1 x 2 x 3 = 6 |
|
|
6 =
1 + 2 + 3 |
|
|
6 =
1 + 2 + 3 = 6 = 3 x 4 / 2 6
/ (1/1 + 1/2 + 1/3 + 1/6) = 6 / 2 = 3 |
Nombre à moyenne
harmonique entière. |
|
6 = 3 + 3 et 3 x 3 =
9 |
|
|
6, 36,
666 6 =
T3 = 1/2 (3x4) = 1 x 2 x 3 |
|
|
6 = 2 + 2 + 2 = 3 + 3 |
|
|
1 + 2 + 3 + 4 + 5 = 7 +
8 = 15 |
|
|
1+2+3+4+5 = 15 //
6
// 7+8 = 15 |
|
|
1,
4, 6, 4, 1 1,
6, 15, 20, 15, 6, 1 |
|
|
6 =
8 – |
|
|
|
|
|
|
|
|
|
|
6 = = |
|
![]()
Table
de multiplication du 6

Voir Table
complète
Multiplication
|
1234 x 6 = 7 404 5050 7404 |
Mettre 5 sous tous les chiffres
impairs. Pour chaque chiffre ajoutez: le chiffre, la valeur 0 ou 5 et la moitié entière du chiffre
précédent. |
|
|
6
x 6 = 36 …6k = … 6 |
|
|
|
6 =
2 x 3 = 1 x 2 x 3 = 3! |
|
|
|
|
|
|
|
6 =
1/2 (3 x 4) |
|
|
|
6!
– 1 = 719 |
|
|
|
6!
= 3! × 5! |
|
|
Division
|
6 =
12 / 2 |
|
||
|
6 est divisible par 1, 2, 3 et 6 et pas par
4 et 5 |
|
||
|
|
|
||
|
|
|||
|
6 =
4! / 2² = 24 / 4 6
= (2 + 2)! / (2! x 2!) |
|||
|
6 6 |
|
||
|
6 6 |
|
||
|
62 – 1 = 35 64 – 1 = 1295 66 – 1 = 46655 … |
|
||
|
|
Ce corps
contient tous les nombres de la forme a + ib |
||
![]()
Diviseurs
|
|
Objet d'une énigme. |
|
6
. k |
|
|
6n |
|
|
6
= |
|
|
Il y a 3 nombres premiers inférieurs à 6 et, 6 est multiple de 3 |
|
|
6
x 26 – 1 = 383 nombre
premier |
|
|
|
|
Puissances

Sommes identiques des chiffres des
puissances
|
62
= 36 |
9 |
65
= 7 776 |
7+7+7+6
= 27 |
67
= 279 936 |
2+7+9+9+3+6
= 36 |
|
63
= 216 |
2+1+6
= 9 |
66
= 46 656 |
4+6+6+5+6
= 27 |
68
= 1 679 616 |
1+6+7+9+6+1+6
= 36 |
|
|
|
|
|
69
= 10 077 696 |
1+0+0+7+7+6+9+6
= 36 |
|
|
|
|
|
610
= 60 466 176 |
6+0+4+6+6+1+7+6
= 36 |
Voir Tables
de telles relations
|
6 =
00 + 11 + 22 |
|
|
|
6 =
1² + 1² + 2² |
|
|
|
6 =
21 + 22 = 23 – 21 = 32 – 31 |
|
|
|
6 = 6² – 5 ² – 3² +
2² = 7² – 6 ² – 4² + 3² = 8² – 7 ² – 5² + 4² = … |
(n–2)² – (n–1) – (n+1) + (n+2) = 6
|
|
|
6 = 54 × 73 – 4632
|
|
|
|
1² + 6x 4 =
5² & 5² + 6x 4 =
7² 2² + 6x16 = 10² & 10² + 6x16 =
14² 3² + 6x36 = 15² & 15² + 6x36 =
21² … |
|
|
|
= 0,53050… + 5,46949… |
Trouvé par H. Dudeney. |
|
|
6 = x3 + y3
+ z3 = (–1)3 + (–1)3 + 23 = …
|
Solutions
du problème de la somme de trois cubes illustrant que dans certains cas les
solutions sont nombreuses (infinies?). |
|
|
6 =
|
|
|
|
6 =
1 + 3/2 + 5/2² + 7/23 + … 6 =
2/30 + 4/31 +
8/3² + … |
|
|
|
6 |
|
|
|
6 |
|
|
|
6 |
|
|
![]()

Identité
impliquant quatre nombres impairs successifs
Voir Brève 61-1218
|
6² = 36
=> 3 + 6 = 9 = 3² 63 = 216 => 2 + 1 + 6 = 9 = 3² |
|
|
65 = 7 776 66 = 46 656 |
|
|
6² =
36 |
|
|
6² =
36 = 1 + 2 + 3 + … + 8 |
|
|
6² =
(1 + 2 + 3)² = 13 + 23 + 33 |
Voir même propriété pour le Nombre 204 |
|
63 = 33 + 43
+ 53 = 216 |
|
|
6 et cubes |
|
|
63 = 216 = 5 x 6
x 7 + 6 =
210 + 6 = 216 |
|
Identité
généralisable
Voir Brève 52-1032
|
64 = 5 x 44 + 24 = 1280 +
16 =1 296 |
|
|
66 =
46 656 68 = 1 679 616 |
|
|
656 = 377…750 656 |
|
|
|
Voir Puissance
de 9 / Nombre de
la Bête / Exposants |
Autour
du 6
Nombre médian d'une suite
équilibrée

Voir Suites équilibrées / Énigme de la
maison du maire
|
|
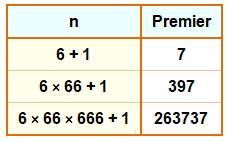
6
+ 1 6
⋅ 66 + 1 6
⋅ 66 ⋅ 666 + 1 6
⋅ 66 ⋅ 666 ⋅ 6666 ⋅ 66666 ⋅ 666666 + 1 6
⋅ 66 ⋅ 666 ⋅ 6666 ⋅ 66666 ⋅ 666666 ⋅ 6666666 + 1 |
|
|
6, 216, 225, 141, 66, 432, 99, 1458, 702, 351, 153 |
|
|
|
1 =
1/2 +1/3 + 1/6 1/6 = 1/2
– 1/3 = 2 (1/3 – 1/4) = 1 – 1/2 – 1/3 |
|
|
|
1/6
= 0,1666 … 4/6 = 0,6666 … 2/6
= 0,3333 … 5/6 = 0,8333 … 3/6 = 0,5 6/6 = 1 |
|
|
|
|
|
|
|
6 x 26 – 1 = 383 est
premier |
|
|
|
…999999… |
|
|
|
1 + 4 = 2 + 3 |
|
|
|
y² = x3 + 6 |
|
|
Jeux et curiosités
|
|
|
|
|
|
|
|
|
|
6
x 1 386 = 8 316 6
x 10 168 = 61 008 6
x 11 386 = 68 316 6
x 11 702 = 70 212 … |
|
Suite Géométrie,
Jeux, Culture…
|
|
Voir Diviseurs, Quantité,
Somme,
Fonctions
arithmétiques
|
Numération: base, [chiffres] |
Repdigit (Brésilien) |
|
|
2,
[1, 1, 0] 3, [2, 0] 4, [1, 2] |
5, [1, 1] 6,
[1, 0] |
5,
[1, 1] |
Voir Bases
/ Brésiliens
![]()
|
Suite |
|
|
Voir |
|
|
Site |
|
|
Cette
page |
![]()