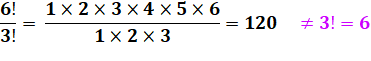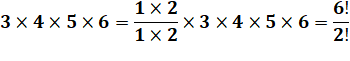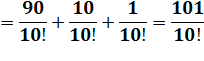|
|||||||||||||||||||||||||||||||||||
![]()
|
FACTORIELLES Débutant et familiarisation Les bases des factorielles
et quelques gammes pour apprendre à les manipuler. |
|
|
|
|
Approche
|
|
|
|
|
|
Définition
n! = 1 x 2 x 3 x … x (n – 1) x n Évidemment le nombre 0 est
exclu!
La factorielle
suivante
(n
+ 1)! = (n + 1) x n! Ex: 6! = 6 x 5! = 6 x
120 = 720 Nombre composé
|
|
|
n = ? |
(n
+ 1)! |
= 6 (n – 1)! |
|
|
Premier membre |
(n
+ 1)! |
= (n + 1) n (n – 1)! |
|
|
Égalité 2e
membre |
6
(n – 1)! |
= (n + 1) n (n – 1)! |
|
|
Simplification |
6 |
= (n + 1) n |
|
|
Équation |
n²
+ n – 6 |
= 0 |
|
|
Astuce! |
n²
+ 3n – 2n – 6 |
= 0 |
|
|
Mise en facteur |
n(n
+ 3) – 2(n + 3) |
= 0 |
|
|
Encore |
(n
– 2) (n + 3) |
= 0 |
|
|
Solutions |
n &
n |
= 2 =
–3 (solution
à rejeter, |
|
Voir Équations
|
La
différence entre deux factorielles successives est égale:
|
3! – 2! = 2 × 2! =
2² × 1! = 4 6! – 5! = 5 × 5! =
5² × 4! = 600
|
|
Voir Brève
807 / Défis
Internet
![]()
|
Suite |
|
|
|
Retour |
|
|
|
Voir |
|
|
|
DicoNombre |
|
|
|
Cette page |
||
![]()