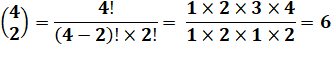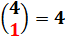|
|||||||||||||||||||||||||||||||||||||||||||||
![]()
|
TRIANGLE DE PASCAL Dénombrement Formules |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Construction
et baptême des lignes et colonnes
Notez:
la
numérotation commence par 0. Remarque importante pour p.
représente
le coefficient de rang p
dans le
développement de (x + y) n.
C(n,k) ou Exemple:
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
Formulation
Remarque:
la notation moderne est plus
logique: le nombre le plus grand est en haut, et il est au même niveau (numérateur)
dans la formule. Voir
Factorielle Exemple:
Formulation
pratique
Exemple:
Voir Calculs
pratiques Formulation
combinatoire
Voir
Combinaisons |
|
|
Observation Avez-vous déjà réalisé que le triangle de Pascal est symétrique: on
retrouve les mêmes nombres à droite comme à gauche sur la même ligne:
Exemple On peut dire de manière équivalente que 4 est la quantité de choix d'un
parfum parmi 4 ou la quantité de choix pour que trois parfums ne soient pas
choisis parmi 4.
Formulation
Il est parfois plus facile de calculer avec celui où le nombre du bas (k
ou n-k) est le plus petit. |
|
Somme des coefficients du
binôme Somme sur une ligne du
triangle de Pascal |
|
||
|
Exemple pratique avec quatre éléments Je dispose de n éléments.
Disons: (a, b, c, d), soit n = 4. Je cherche à savoir quelle
est la totalité des combinaisons de ces éléments pris 1 par 1, puis 2 par 2,
puis 3 par 3 et enfin 4 par 4. L'ordre est sans importance. La quantité de combinaisons se
calcule comme suit, par exemple pour 2 éléments pris parmi 4:
En pratique: 2 termes au numérateur
comme au dénominateur. En haut, on part du plus grand (ici:4) et en bas de 1. |
|||
|
J'en
choisis 0 |
1 possibilité |
|
|
|
J'en
choisis 1 parmi 4 |
4 possibilités: a, b ,c, d |
|
|
|
J'en
choisis 2 parmi 4 |
6 possibilités: ab, ac, ad, bc, bd, cd |
|
|
|
J'en
choisis 3 parmi 4 |
4 possibilités: abc, abd, acd, bcd |
|
|
|
J'en
choisis 4 parmi 4 |
1 possibilité: abcd |
|
|
|
Analogie avec le développement du binôme On reconnait naturellement
les coefficients
du binôme, lesquels nous donnent le développement de (a + b) à la
puissance 4: (a + b)4 = a4
+ 4a3b + 6a2b2 + 4ab3 + b4 La formule générale du développement
du binôme est la suivante:
On lit: a plus b
à la puissance k est égal à la somme pour chacune des valeurs de i depuis 0
et jusqu'à k du produit des coefficients du binôme (k, i) de a à la puissance
k moins i et de b à la puissance k. Nous cherchons à connaitre
la somme de ces coefficients. Pour faire disparaitre les a
et b, il suffit de leur donner la valeur 1: (1 + 1)4 = 1 + 4 +
6 + 4
+ 1 = 24 = 16 Cas général Rien n'empêche de
généraliser à n'importe quelle puissance:
On retrouve la propriété
connue: la somme des nombres sur la ligne k du triangle
de Pascal vaut 2k. La somme des combinaisons de
k éléments pris 1 par 1, puis 2 par 2, puis… k par k est égale à 2k.
Si j'élimine le cas trivial où je ne prends rien, la somme devient 2k
– 1 La somme des combinaisons à partir de k éléments
est égale à 2k. Exemple Par exemple avec k = 16, il y
a un total de combinaisons égale à 216 = 65 536 Et, 65 535 en éliminant le
cas où on ne prend rien. Quantité selon les cas:
Il y a, par exemple, 8 008 possibilités de prendre 6 éléments parmi
16, même quantité pour 10 éléments parmi 16. La ligne est symétrique. |
|||
Voir Triangle de Pascal
pour autres cas
![]()
|
Suite |
|
|
Voir |
|
|
Aussi |
|
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/Iteration/TrgPasc1.htm
|
![]()