NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 20/02/2023 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	ITÉRATIONS
Débutants Général	TRIANGLE de PASCAL				Glossaire Général
INDEX Itérations	Approche	Formules	Propriétés	Historique
	Triangle	Valeurs	Fractal	Puissance 11
	Angle en Pi / n	Binôme	Divisibilité	Programmation
	Sommaire de cette page >>> Le taxi en ville >>> Triangle de Pascal – Introduction >>> Triangle de Pascal – Développement du binôme >>> Puissances de 11

Autres triangles

Index – Triangles	En géométrie	Des nombres	De Leibniz	Autres
	Triangle des modulos

TRIANGLE de PASCAL

ou triangle arithmétique

ou triangle de Stifel

Cette page est une introduction

Hep! Je voudrais simplement les valeurs du triangle de Pascal

Pour un triangle développé jusqu'à la ligne 12 >>>

Pour un triangle plus complet >>>

Pour le calcul et les formules >>>

Voir Historique, Stifel 

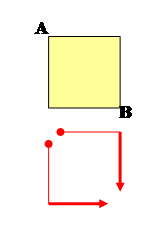
LE TAXI EN VILLE (Manhattan) Combien de chemins entre A et B, les plus courts possibles ?
Avec 1 cellule Il y a deux chemins

Avec 2 cellules Il y a trois chemins
Avec 3 cellules Il y a quatre chemins
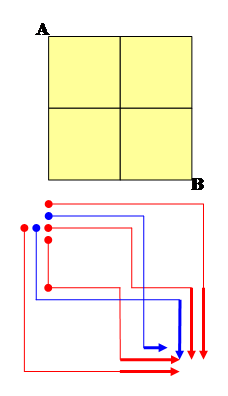
Avec 2 x 2 cellules Il y a six chemins

Voir Escalier / Chemins sur réseau (Manhattan) / Nombres de Delannoy

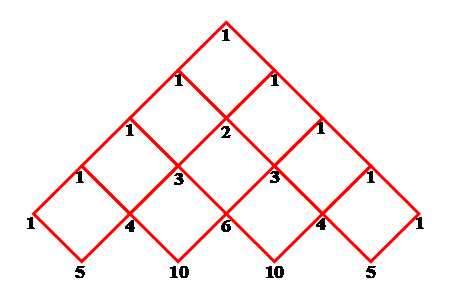
Généralisation
Avec n x p cellules, il y a autant de chemins que le nombre correspondant dans le triangle de Pascal. Découvrons la construction du triangle de Pascal.

TRIANGLE DE PASCAL – Introduction

Approche

Voyons le tableau suivant:

Observez la cascade qui se construit en ajoutant les deux nombres du dessus. Lorsque le nombre est seul, le manquant est considéré comme nul.

Autre présentation

1	1	1	1	1	1	1	1	1	1
1	2	3	4	5	6	7	8	9
1	3	6	10	15	21	28	36
1	4	10	20	35	56	84
1	5	15	35	70	126
1	6	21	56	126
1	7	28	84
1	8	36
1	9
1

Chaque nombre est la somme de son voisin du haut et de celui de gauche
Exemples: 6 =3 + 3; 10 = 6 + 4; 15 = 10 + 5 ; etc.

Voir Triangle Pascal jusqu'au rang 30 et plus

Triangle de Pascal

ou triangle arithmétique (comme l'appelait Pascal)

ou triangle d'al Karaji (mathématicien arabe)

Tableau de nombres baptisé d'après Blaise Pascal (1623-1662), qui rédigea un traité sur le triangle arithmétique vers 1650.

Mais connu bien avant lui par les Arabes, dès le XI^e siècle

Les nombres correspondent aux coefficients des développements des puissances successives de x + y,
C'est-à-dire de:

(x + y)¹ (x + y)² ... (x + y)ⁿ

Voici le début de ces expressions avec comparaison avec les valeurs des nombres du triangle de Pascal:

Triangle de Pascal						Développements
1	1					(x + y) ^1	=	x + y
1	2	1				(x + y) ^2		x² + 2xy + y²
1	3	3	1			(x + y) ^3		x^3 + 3x^2y + 3xy^2 + y^3
1	4	6	4	1		(x + y) ^4		x^4 + 4x^3y + 6x²y² + 4xy^3 + y^4
1	5	10	10	5	1	(x + y) ^5		x^5 + 5x^4y + 10x^3y^2 + ...

On constate que chaque coefficient est bien la somme des deux au-dessus:

Exemple: 10 = 6 + 4

Petit truc: la somme des exposants d'un monôme est égale au degré de l'expression de départ:

Exemple: 10x³y² => 3 + 2 = 5 ; 5 de (x + y) ⁵

Voir Formule du binôme

Puissance de 11
La suite est toujours conforme au triangle de Pascal à condition de tenir compte des retenues. L'exemple montre une façon de disposer les calculs:

Voir Nombre 11 / Repunit

Suite	Triangle de Pascal – Formules
Voir	Combinaisons Famille de 1 à 10 enfants Formule du binôme Pascal – Biographie Petit théorème de Fermat Factorielle et triangle de Pascal Triangle de Pascal et relation de Fermat Triangle premier Triangle – Index
Aussi	Boucle infernale Calcul mental Géométrie – Index Nombres de Stirling Récurrence Théorie des nombres
Graphes	Graphes et chemins optimums Parcours des abeilles Voyageur de commerce
DicoNombre	Nombre 11 Nombre 121	Nombre 1 331 Nombre 14 641
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Iteration/TrgPasca.htm