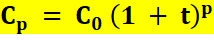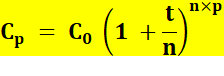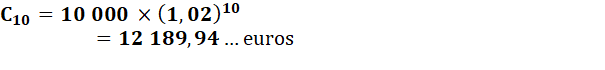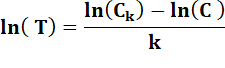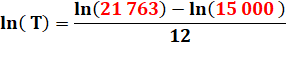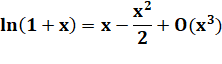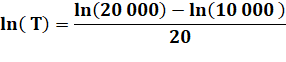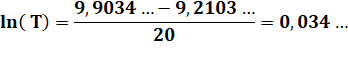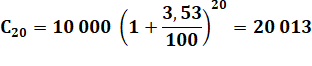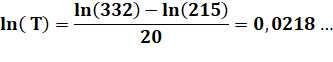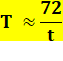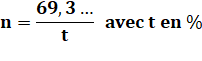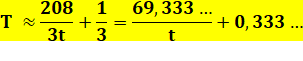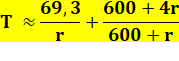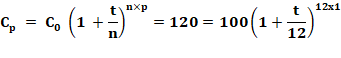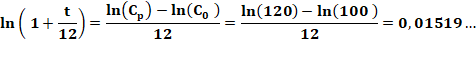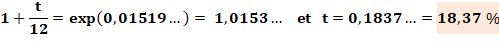|
||||||||||||||||||||||||||||
![]()
|
Calculs d'intérêts composés Je place mon argent. Mon
capital s'enrichit des intérêts. Combien cela me rapporte-t-il? Autre situation: me voilà en
fin de période. À quel taux d'intérêt correspond le capital final versé?
Utilisation pratique d'un tableur pour éviter l'emploi d'outils mathématiques
trop compliqués. On explique néanmoins comment s'y prendre avec une
calculette et les boutons log et exp. |
|
Je
vous prête 1000 euros que vous devrez me rembourser à raison de 100 euros par
mois durant un an. Quel est le taux d'intérêt annuel? Eh
bien, 12%, facile ! Non, ce sont des intérêts composés. Anglais: if I gave you €100 today and you
paid me back €10 every month for a year, what is the annual interest rate on
your loan? |
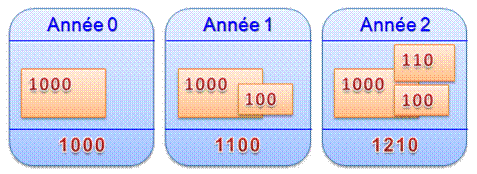
Intérêts Composés
Que deviennent 1000 euros
placés à 10 % ?
Formule fondamentale
|
Capital plus intérêts au bout de deux ans: 1210 euros |
|
Note: t est le taux comme par exemple 0,05 pour 5%
|
Avec un
taux de croissance de 1%, le doublement intervient en 72 ans (environ). Avec un taux
de croissance de 2%, le doublement intervient en 72/2 = 35,5 ans. Avec un
taux de croissance de 10%, le doublement intervient en 72/10 = 7,2 ans. Avec un
taux de croissance de t %, le doublement intervient en 72 / t années. |
Voir Explications
/ Nombre 72
![]()
|
|
||
|
Approche Je
dispose d'une somme d'argent (capital) que
je dépose à la banque pour celui-ci me rapporte des intérêts. L'intérêt est la somme d'argent que la banque me versera pour
chaque 100 euros de capital placé, et cela chaque année. Un
intérêt composé veut dire que chaque année
les intérêts sont ajoutés à mon capital. Les
intérêts de l'année suivante sont calculés sur la base du capital et de tous
les intérêts cumulés. |
Capital:
C = 10 000 € Intérêt:
t = 5% (ou 0,05) Intérêts
à la fin de la première année: I = C . t = 10 000 x 5% = 500 C1
= 10 000 + 500 = 10 500 € Intérêts
à la fin de la deuxième année: I = C1 . t = 10 500 x 5% = 525 C2
= 10 500 + 525 = 11 025 € |
|
|
Formulation générale Le
capital Cp acquis à partir d'un capital initial C0 au bout de p
années avec un intérêt t est donné par la formule => Si
la période de calcul des intérêts est une énième partie de l'année, la
formule devient => Si
le taux varie selon les années, la formule doit être adaptée, année par année
=> |
Pour 6 mois, n = 2 Pour 3 mois, n = 4
|
|
|
Capital:
10 000 € sur 2 ans à 5% composés. |
Cf = 10 000 (1 + 5%)² = 10 000 x 1,1025 = 11 025 |
|
Capital
initial: 350 111 à 4% composés |
409 580 = 350 111
(1 + 4%) p 1,04 p = 409 580 / 350 111 = 1,169
858 Or 1,042
= 1.081 6 1,043 = 1.124 864 1,044 = 1.169 858 Bingo Placement sur 4 ans |
|
Le
capital double en 4 ans. Combien d'années pour un capital multiplié par 8 ? Si un capital est multiplié par k en p années, il croit kn fois
en n.p années. |
Calcul Le capital
double en 4 ans (2C). Ce capital
(2C), placé sur 4 ans, va doubler (4C). Ce capital
(4C), placé sur 4 ans, va doubler (8C). Le capital
atteint 8C après trois périodes de 4 ans, soit 12 ans. |
|
|
||
|
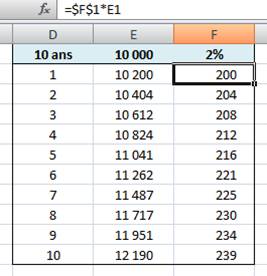
Calcul de la somme finale Supposons un placement de 10 000 euros à 2% par an sur
une durée de 10 ans. 1. Placez ces valeurs
en D1, E1 et F1. Pour avoir
le %, utilisez la boite de dialogue "nombre" et choisissez %. 2. 3. En F2, donnez la
formule de calcul: multiplier F1 (l'intérêt) par E1 (la somme d'argent). Pour que
F1 (2%) soit toujours utilisée, montrez F1 avec la souris puis tapez sur F4
(touche de fonction) F1 devient $F$1. |
Voir Programmation |
|
|
4. En E2, mettre la
formule de calcul: = E1+F2 (capital plus intérêt). 5. Soulignez E2 et F2
puis tirez sur la poignée en bas à droite, vers le bas jusqu'au 10 ans. 6. Mettre en forme à
loisir. Au bout de 10 ans, la somme placée est devenue 12 190
euros, valeur que l'on retrouve avec la
formule:
|
||
|
Calcul de l'intérêt à partir
de la somme finale Une somme de 15 000 euros a été placée durant 12 ans.
La banquier m'avait indiqué un taux. Mais depuis, les frais de gestion et les
taxes ont été modifiées; Finalement, à échéance, le banquier me sert une
somme de 21 763 euros. Gain: 6 763, soit 45,09 % d'augmentation du capital Intérêt moyen: 45,09 / 12 = 3,757%. Je cherche un calcul plus précis de l'intérêt composé. |
|
|
Je reprends le tableau précédent. J'adapte le tableur:
12 ans et 15 000 euros au départ. Puis, par essais successifs, j'ajuste la valeur de
l'intérêt dans F1 pour obtenir 21 763 euros en E13. La valeur du taux vaut
alors 3,15 %. Je souhaiterais un
calcul direct avec une formule? D'accord, mais il
va falloir passer aux logarithmes!
|
|
|
Calcul formel du taux – (logarithmes et exponentielles) |
|
|
|
On reprend la formule générale en
adoptant: T = 1 + t. Ck est le capital acquis
après k années et C est le capital initial. |
|
|
|
Passage aux logarithmes népériens. (Pour pouvoir utiliser
l'exponentielle, sa fonction réciproque) |
|
|
|
Propriété
des logarithmes: |
|
|
|
Propriété
des logarithmes: |
|
|
|
Nous cherchons
le taux T. |
|
|
|
Passage aux valeurs numériques. Rappel du problème: 15 000 euros placés
durant 12 ans deviennent 21 763. Quel est le
taux composé? |
|
|
|
Passage aux exponentielles,
en se souvenant
que exp(ln(T)) = T. |
|
|
|
Retour au taux d'intérêt (t = T –
1). Et en pourcentage arrondi: |
t
= 3,15 % |
|
|
En pratique Le
calcul des logarithmes et des exponentielles est disponible sur la calculette de
votre ordinateur. Pour
le logarithme, introduire votre nombre avec le clavier numérique et appuyez
sur ln. Pour
l'exponentielle, introduire votre nombre, appuyez sur la flèche
(illustration) et sur ex. |
|
|
|
Note On
ne sera pas étonné de la proximité des décimales car le logarithme de 1 + x
est très voisin de x pour x petit. O(x3) indique que le terme
suivant est du troisième dégré (ici, négligeable). |
|
|
|
Bonus pour s'exercer Je
souhaite que mon capital de 10 000
euros soit doublé en 20 ans. Quel est le taux à appliquer? Note de calcul: ln(20
000) – ln(10 000) = ln(20000/10000) = ln(2) = 0,6931… |
Résolution
Vérification
|
|
Bureaucratie à la française ! Les
Dix Commandements: 68 mots. La
déclaration d'indépendance américaine: un feuillet. Ordonnance
de la Communauté européenne sur les importations de caramels: 25 911 mots. Droit
français en 2021: 331 848
articles législatifs et réglementaires pour 215 202 en 2001, soit +54 % en 20
ans. Mais
quel pourcentage par an ? |
Résolution
|
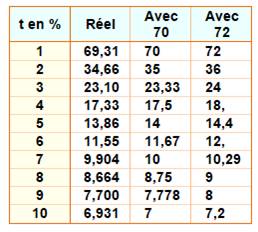
Table:
intérêts composés sur 3 ans pour un taux de 1 à 10 %

|
|
||
|
Capital 15 000
euros à 3% sur 2 ans. 15 000
euros à 3% sur 3 ans. |
C(3%, 2) = 15 000 x 1,0609 = 15 913,50 C(3%, 3) = 15 000 x 1,092727 = 16 390,90 |
|
|
15 000
euros à 2 % la première année, puis à 3 % les 2 prochaines années. Capital à
l'issue des 3 ans? |
C = 15 000 (1 + 2/100) (1 + 3/100)2 = 15 000 x 1,02 x 1,0609 = 16 231,77 euros |
|
|
Si 4 800
deviennent 6 000 en 4 ans, quelle sera le capital après 12 ans? |
4 800 (1 + t/100)4 = 6 000 (1 + t/100)4 = 6 000 / 4 800 = 5 / 4 (1 + t/100)4x3 = (5 / 4)3 = 125 / 64 Après 12 ans: 4 800 (1 + t/100)12 = 4 800 x 125 / 64 = 9 375 euros |
|
|
Durée 5 000 à 3
% produisent 5 304,50 euros. Durée? |
5 000 x (1 + 3/100)p = 5 304,50 (1 + 3/100)p = 5
304,5 / 5000 = 1,0609 Réponse : 2 ans (lecture dans le tableau). |
|
|
Durée en
années pour que ma somme placée 10 % me rapporte plus du double? |
C x (1 + 10/100)p > 2C (1,1)p > 2 (1,1)7 = 1,95 (1,1)8 = 2,14 Réponse: 8 ans Valeur exacte: 7,27 ans (= ln2 / ln1,1) |
|
|
Mon
capital triple en 3 ans. Dans combien de temps aurai-je 9 fois mon capital
initial? Raisonnement
intuitif: le capital triple acquis après 3 ans est
replacé pour 3 ans. Sa valeur triple. Bilan: le capital acquis est multiplié
par 3x3 = 9 en deux périodes de 3 ans, soit 6 ans. |
C x (1 + t/100)3 = 3
C (1 + t/100)3 = 3 { (1 + t/100)3 }² = 32 = 9 (1 + t/100)6 = 9 C(1 + t/100)6
= 9C Réponse: en 6 ans |
|
|
Taux Je
dispose de 9 fois le capital en 2 ans. Quel est le taux? |
C(1 + t/100)2 = 9C (1 + t/100)2 = 9 = 32 1 + t/100 = 3 t = 2 x 100 = 200 % |
|
|
Mon
capital de 80 000 euros produit une somme 88 200 euros en 2 ans. Quel est le
taux? |
88 200 = 80 000 (1 + t/100)2 (1 + t/100)2 = 88 200 / 80 000 = 1,1025 Réponse : 5 ans (lecture dans le tableau). |
|
|
Intérêts Quel est l'intérêt servi à partir d'un capital de 15 000 euros
placés à 4 %, puis 5 % et enfin à 6 % sur 3 ans? |
CI = 15 000 (1+4/100)(1+5/100)(1+6/100) – 15 000 = 17 362,80 – 15 000 = 2
362,80 euros |
|
|
|
||
|
Méthode
pour estimer rapidement le doublement d'un placement, ou toute chose
croissante. La règle
des 72 est utilisée depuis la Renaissance (Luca Pacioli – 1494). |
Soit t le taux de croissance Et T la durée en années (ou périodes) de la
croissance pour obtenir un doublement:
|
|
|
Formule
des intérêts composés pour n périodes et un doublement. Calcul
avec le logarithme. |
|
|
|
Avec de
faibles taux d'intérêt: |
|
|
|
La
formule devient: |
|
|
|
Approximation
avec 70 pour de très faibles taux. L'approximation avec 72 pour des taux de 5
à 10% avec plus de facilité pour le calcul mental .
Le
tableau montre les valeurs selon la formule utilisée. |
|
|
|
Une
meilleure approximation: |
|
|
|
Une autre
(approximation de Padé): |
|
|
2
|
|
|
|
Money is said to be lent at compound
interest when at the end of the year (or other fixed period) the
interest that has become due is not paid to the lender, but is added to the
sum lent, and the amount thus obtained becomes the principal
for the next period. The process is repeated until the amount for the last period has been
found. The difference between the original principal and the final amount is
called compound interest. |
|
|
Énigme Je
vous prête 1000 euros que vous devrez me rembourser à raison de 100 euros par
mois durant un an. Quel est le taux d'intérêt annuel? Solution N'y
connaissant pas grand-chose en maths, j'utilise un tableau et j'ajuste le taux pour
arriver à 120 avec un capital de départ de 100.
Chaque
mois le nouveau capital est augmenté des intérêts du mois. On a bien un
intérêt composé jouant mois après mois. Avec les formules (vues ci-dessus) Formule
générale
Mise
en forme pour calculer t
|
![]()
|
Suite |
|
|
Voir |
|
|
Aussi |
|
|
Sites |
|
|
Livre |
|
|
Cette page |
http://villemin.gerard.free.fr/aEconomi/aaaFINAN/Compose.htm |
![]()